Por David Galadí Enríquez

Nada hay más fácil de ver en el cielo que nuestra querida Luna. Y esto es cierto tanto de día como de noche. Por más que de día llame la atención el Sol, no resulta nada cómodo observarlo porque la fuerza de su brillo ciega, puede hasta provocar lesiones en los ojos, incluso cuando se observa a simple vista. La Luna, sin embargo, no le hace daño nunca a nadie.

¿Tanto de día como de noche? Pero ¿la Luna no es el astro de la noche? ¿Cómo es eso de que también se puede ver de día? Pues así es. Disculpe el comentario tan elemental, si usted ya se había dado cuenta antes de que la Luna, muy a menudo, se ve de día, pero puedo asegurarle que hay muchas personas en este mundo moderno que no lo han hecho y que aún se extrañan al recibir esta afirmación.

Cuando la Luna está por encima del horizonte en una noche despejada no hay manera de esquivar su visión. Por mucha contaminación lumínica que haya, nuestro satélite natural destaca siempre contra el fondo (más o menos) oscuro del firmamento nocturno. Durante el día la luz del Sol ilumina la atmósfera terrestre y le confiere ese brillo azul celeste que oculta de nuestra vista casi todo lo que hay detrás. Cuando la Luna aparece en el cielo durante el día puede costar algo más darse cuenta de que está ahí, pero se puede ver sin problemas, si el cielo está limpio de nubes y de calimas.

De acuerdo, ya lo sabemos: la Luna aparece de vez en cuando en el cielo, a veces de día y en otras ocasiones de noche, y además cambia de forma, desde una finísima tajadita de melón a una magnífica Luna llena, redonda y resplandeciente. Pero ¿hay algún orden detrás de todo esto?

Distancia y tamaño

Lo primero que cabría preguntarse es cómo de grande es la Luna. La vemos en el cielo como un disquito o una bolita de cierto tamaño aparente, pero ¿cuánto mide de verdad? La respuesta no es sencilla de obtener y, de hecho, la observación a simple vista y con medios sencillos aporta muy poca información al respecto.

Empecemos por lo más obvio. ¿Cuánto mide la Luna en el cielo? Ya en la entrega anterior de esta guía, dedicada a la orientación de día y de noche, introdujimos un método simple para medir ángulos en el cielo. Si una vuelta entera al firmamento abarca 360 grados, entonces una regla sostenida a 60 cm del ojo hace que cada centímetro corresponda a un grado, y resulta que 60 cm viene a ser la distancia promedio a la que queda la mano cuando se extiende el brazo (compruébelo por sus propios medios). Nos planteamos, por tanto, cuánto abarca la Luna en el firmamento cuando se mide con una regla sostenida con el brazo extendido.

La respuesta suele sorprender a muchas personas que se inician en la astronomía. La Luna, medida en estas condiciones ¡cubre bastante menos de un centímetro! De hecho abarca medio centímetro, es decir, el disco lunar mide medio grado.

Si recordamos de nuestros tiempos en la escuela que cada grado se divide en sesenta minutos de arco, podríamos decir también que el disco lunar abarca treinta minutos de arco (aproximadamente).

Hasta ahora todo bien (salvo, quizá, la sorpresa de descubrir que la Luna se ve tan pequeña en el cielo: salga con la regla y haga la prueba). Pero ¿qué nos dice esto sobre el tamaño real, físico, verdadero de la Luna, expresado por ejemplo en millas o en quilómetros? Pues nada, no nos dice nada.

Porque el tamaño angular aparente de un objeto, como ese medio grado que abarca la Luna, resulta de combinar las dimensiones físicas lineales del cuerpo con su distancia al observatorio. Dicho de otro modo, la Luna podría ser un objeto muy pequeñito pero situado muy cerca, o bien uno muy grande ubicado lejísimos. Si observamos la tabla 1 podemos comprobar que casi cualquier cosa de la vida cotidiana puede adoptar el mismo tamaño angular aparente de la Luna si se coloca a la distancia adecuada. Una moneda de veinte pesos debería ubicarse a 3.3 metros, una vaca (si se considera esférica en primera aproximación, como es habitual) a 166 metros. Si se recortara de la superficie terrestre la isla de La Española o un país como Uruguay (vienen a medir lo mismo, unos 500 km) habría que mirarlos desde más de 55 000 km para que cubrieran la Luna por completo: más allá de la órbita en la que se mueven los satélites geoestacionarios.

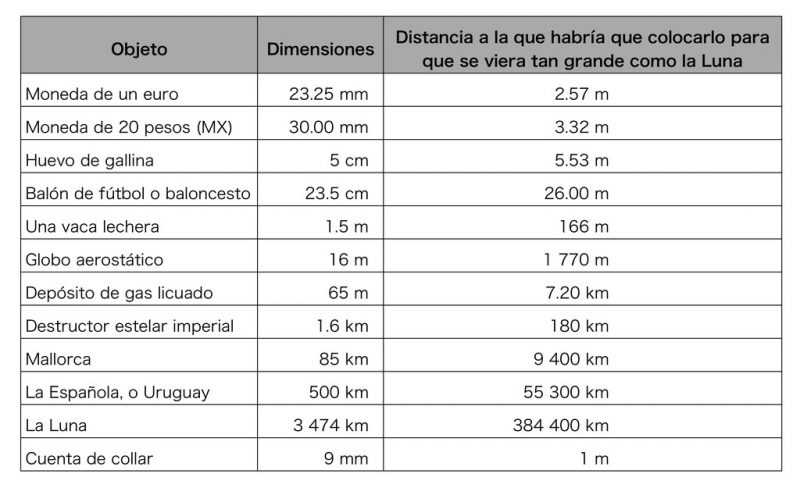
Tabla 1. Varios objetos más o menos cotidianos y las distancias a las que habría que situarlos para que mostraran el mismo tamaño aparente que la Luna.

Hay métodos simples y muy fiables para medir la distancia a la Luna. El más sencillo de entender consiste en elegir dos observatorios separados por una distancia conocida (supongamos, por ejemplo, Barranquilla y Bogotá, lugares entre los que median unos 660 km) y mirar desde ellos la Luna al mismo tiempo: desde cada punto de la Tierra se verá la Luna en un lugar ligeramente distinto del firmamento y, al medir esa diferencia, se puede deducir la distancia. Este método es tan sencillo que permitió conocer el valor aproximado de la distancia a la Luna ya incluso en la antigüedad clásica. Sabemos hoy que esa distancia, en promedio (porque varía un poco a lo largo del mes), asciende a 384 400 km.

Figura 1. Una moneda de 20 pesos (MX); colocada a 3.32 metros de distancia presenta el mismo tamaño aparente que la Luna llena. www.banxico.org

Obsérvese la última entrada que hemos añadido a la tabla, la que se refiere a una cuenta de collar de 9 mm de diámetro. Ha querido la buena fortuna que una bolita de casi un centímetro aparezca tan grande como la Luna cuando se coloca del ojo a una distancia justa de un metro. Más adelante sacaremos partido a esta coincidencia tan agradable y que se puede resumir en que cualquier cosa se parece a la Luna si se sitúa a una distancia igual, más o menos, a unas cien veces su diámetro (en rigor, 111 veces, pero la diferencia no es relevante para nuestros fines).

Una bola a la luz del Sol

Sabemos que la Luna es una esfera sólida que no emite luz propia, sino que debe todo su brillo aparente a la luz que refleja procedente del Sol. Justo a eso se deben los cambios de forma de su parte iluminada. No cuesta nada reproducir el fenómeno a escala poniendo a la luz del día una pelota de cualquier tipo, preferiblemente de algún color liso y claro. Según el juego de direcciones formado por la posición del Sol y de la pelota respecto de la persona que observa, se comprueba que la parte iluminada del balón va cambiando de forma y es posible reproducir así el aspecto de todas las fases lunares.

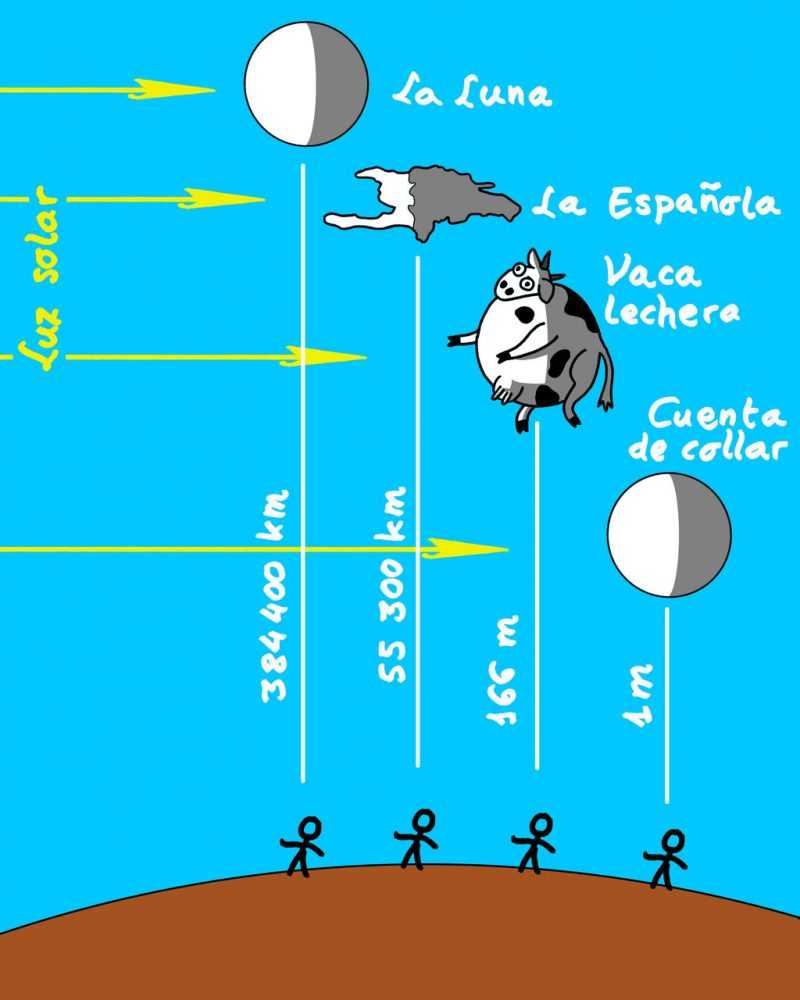
Figura 2. Algunos objetos de la tabla 1, colocados de manera que reproduzcan el tamaño aparente y la fase de la Luna.

Si el balón es de fútbol o baloncesto y se sostiene con la mano, entonces lo tendremos a unos 60 cm del rostro y su tamaño aparente será muchísimo mayor que el de la Luna. Pero si volvemos a consultar la tabla 1 se comprueba que bastaría situar la pelota a 26 metros de distancia para que su diámetro angular igualara el de nuestro satélite natural. No resulta práctico hacer experimentos con cosas situadas tan lejos, así que… ¿qué tal si, en lugar de un balón, tomamos una cuenta de collar de 9 milímetros de diámetro? Se puede colocar al final de un listón de madera de un metro de longitud y así, al poner el ojo en una punta del palo se obtendrá una visión de la bolita que iguala el diámetro aparente de la Luna observada desde la Tierra. Ahora sí podemos jugar, a plena luz, a apuntar hacia distintas direcciones y comprobar el cambio de aspecto de una bolita que emula en muchas cosas lo que hace la Luna en el firmamento de la Tierra.

Solo falta ahora que hagamos el experimento un día (soleado y claro) en el que también la Luna esté a la vista. En un sitio bañado por la luz solar, proceda a apuntar hacia la Luna con el listón de un metro que lleva la bolita en el extremo. Efectivamente: la cuenta de 9 milímetros no solo emula la Luna en cuanto a tamaño, sino que, además, exhibe exactamente la misma fase que ella. ¿Casualidad? ¿Magia?

Aunque no vamos ahora a explicar cómo se sabe, el caso es que el Sol está unas 400 veces más lejano que la Luna. Eso quiere decir que la distancia que media entre la Tierra y la Luna es tan pequeña comparada con la que hay hasta el Sol que puede despreciarse para cualquier experimento realizado a simple vista. O, dicho de otro modo, la Luna (allí «lejos») y la bolita de collar (aquí en la Tierra) reciben la luz del Sol desde la misma dirección. Por eso, si alineamos la cuenta con la Luna y la colocamos a un metro (lo que iguala los tamaños aparentes), el resultado es visualmente idéntico. Lo mismo ocurriría si en lugar de colocar una cuenta de collar de 9 milímetros a un metro, hiciéramos pruebas con cualquiera de los otros objetos de la tabla 1, cada uno situado a la distancia que le corresponde para subtender un ángulo de medio grado.

Figura 3. La bolita de 9 mm situada a 1 m de distancia y orientada, de día, hacia la Luna, presenta la misma fase.

Ahora disponemos de una herramienta para simular el ciclo completo de las fases lunares: basta ir jugando a plena luz del día con el bastón de un metro y comprobar que cuando la bolita pasa, más o menos, entre el ojo y el Sol, entonces solo llega a verse su cara no iluminada. Por el contrario, al dirigir el listón en sentido opuesto al Sol (si se evita que pase por la sombra arrojada por la cabeza) se disfruta de una magnífica simulación de la Luna llena. Las fases de cuarto, por supuesto, resultan cuando las direcciones al Sol y a la bolita de 9 milímetros forman ángulos rectos.

Figura 4. Algunas fases lunares reproducidas con la cuenta de collar de 9 mm a la luz del Sol. Izquierda: fase casi llena. Centro y derecha: fases de cuarto.

Las fases: desde el norte y desde el sur

Este puede ser un buen momento para constatar que la Luna no se ve igual desde los dos hemisferios de la Tierra. Aunque la orientación del disco de la Luna visto contra la esfera celeste depende de muchas cosas, en general es verdad que cuando se mira desde el hemisferio norte terrestre, entonces la Luna presenta su zona norte más o menos en la parte de arriba del disco visible, mientras que desde observatorios situados en el hemisferio terrestre austral es la zona sur de la Luna la que se ve en la parte alta de su imagen.

Figura 5. La Luna muestra orientaciones aparentes opuestas cuando se observa desde hemisferios distintos de la Tierra (norte o sur).

El motivo no es otro, en el fondo, que la forma redonda de la Tierra, que hace que la línea vertical apunte en cada hemisferio, más o menos, hacia la dirección general del polo terrestre correspondiente a esa mitad del planeta.

Dado que la Luna se ve con orientaciones invertidas desde los hemisferios norte y sur, tal vez convenga plantear la explicación de sus fases por separado para cada parte de la Tierra. Sucede que la mayoría de hablantes de castellano habitan el hemisferio boreal, lo cual quizá no sea una mala excusa para empezar por el norte.

Fases lunares para observatorios boreales

Observemos el sistema Tierra-Luna colocando el punto de vista más o menos por encima del hemisferio norte y supongamos que el Sol se encuentra hacia la derecha del campo de visión, a una distancia igual a unas cuatrocientas veces la separación entre nuestro planeta y su satélite. En estas condiciones la Luna recorre una órbita en torno a la Tierra en sentido antihorario.

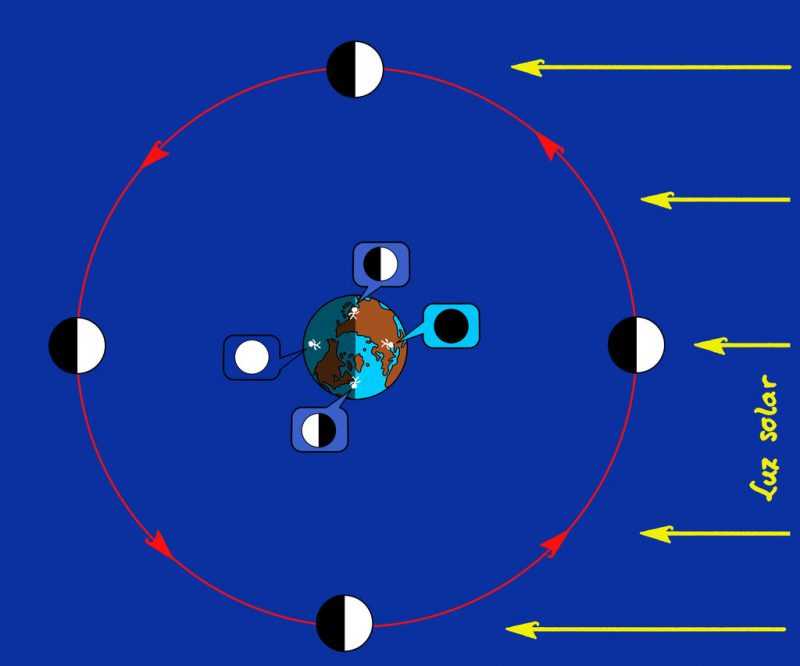
Figura 6. Fases lunares para un observatorio boreal. Derecha: novilunio. Arriba: cuarto creciente. Izquierda: plenilunio. Abajo: cuarto menguante.

Imaginemos una situación de partida en que la Luna se encuentre más o menos entre la Tierra y el Sol. La Luna recibe la luz solar sobre la cara de atrás, la opuesta a la Tierra, de modo que desde el planeta vemos el disco lunar oscuro. Esta fase recibe el nombre de Luna nueva o novilunio.

A partir de ahí, día tras día la Luna avanza en la órbita «hacia la izquierda» (tanto en la figura 6 como sobre el cielo) y va recibiendo un poquito de luz solar sobre la parte derecha del disco, que pasa a verse como una delgada tajadita de sandía con la barriga siempre orientada hacia la posición del Sol, y siempre al ponerse el Sol o en la primera parte de la noche. Completado el primer cuarto de vuelta, la mitad derecha del disco lunar aparece iluminada y esta fase se denomina cuarto creciente: aunque se vea la mitad (y no un cuarto) de disco iluminado, el satélite ha completado un cuarto de vuelta y, además, en el curso de estos días su parte brillante ha ido creciendo.

Y lo sigue haciendo. Pasado el primer cuarto, el avance de la Luna provoca que cada vez haya más luz en la parte que se ve desde la Tierra hasta que, al completar media vuelta, todo el disco aparece iluminado: estamos en Luna llena o plenilunio. A partir de ahí la parte iluminada empieza a reducirse, o a menguar, con una porción oscura de disco lunar que se va extendiendo desde la derecha hacia la izquierda. En el tercer cuarto de vuelta ya solo queda medio disco iluminado (la mitad izquierda) y se alcanza el cuarto menguante.

Solo queda un cuarto más de vuelta hasta volver a la fase de Luna nueva y durante ese tiempo la parte brillante del disco lunar se reduce hasta quedar convertida, otra vez, a una lúnula finísima que solo se ve un ratito antes del alba.

Fases lunares para observatorios australes

Si se observa el sistema Tierra-Luna colocando el punto de vista más o menos por encima del hemisferio sur se obtiene un cuadro parecido al del apartado anterior, aunque algunas cosas cambian de orientación. Ahora, por ejemplo, la Luna recorre una órbita en torno a la Tierra en sentido horario. Procedemos a repetir la descripción del apartado anterior, cambiando lo que sea necesario para encajar con lo que se ve desde emplazamientos australes.

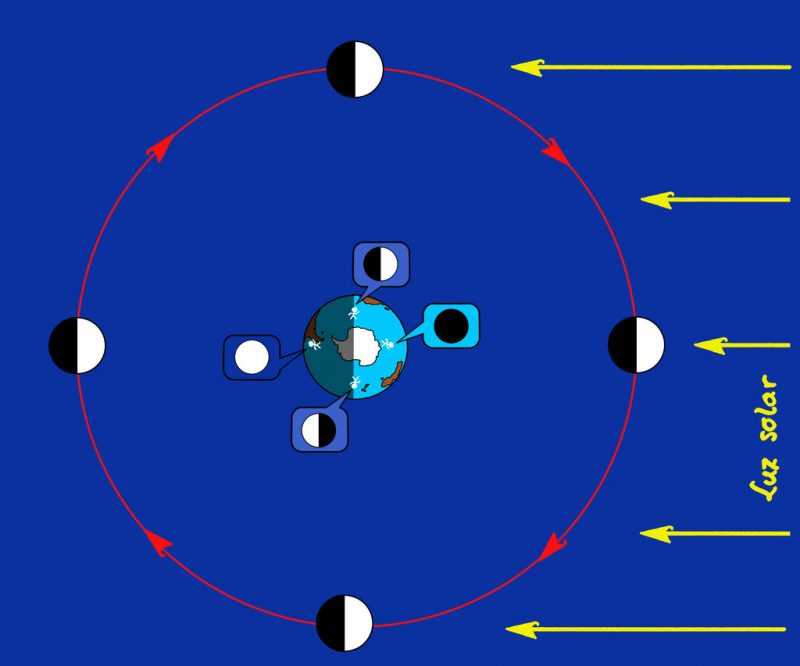
Figura 7. Fases lunares para un observatorio austral. Derecha: novilunio. Abajo: cuarto creciente. Izquierda: plenilunio. Arriba: cuarto menguante.

Volvemos a partir de la situación en que la Luna se encuentra entre la Tierra y el Sol. La Luna recibe la luz solar sobre la cara de atrás, la opuesta a la Tierra, de modo que desde el planeta vemos el disco lunar oscuro. Esta fase recibe el nombre de Luna nueva o novilunio.

A partir de ahí, día tras día la Luna avanza en la órbita «hacia la derecha» (tanto en la figura 7 como en el firmamento) y va recibiendo un poquito de luz solar sobre la parte izquierda del disco, que pasa a verse como una delgada tajadita de sandía con la barriga siempre orientada hacia la posición del Sol, y siempre al ponerse el Sol o en la primera parte de la noche. Completado el primer cuarto de vuelta, la mitad izquierda del disco lunar aparece iluminada y esta fase se denomina cuarto creciente: aunque se vea la mitad (y no un cuarto) de disco iluminado, el satélite ha completado un cuarto de vuelta y, además, en el curso de estos días su parte brillante ha ido creciendo.

Y lo sigue haciendo. Pasado el primer cuarto, el avance de la Luna provoca que cada vez haya más luz en la parte que se ve desde la Tierra hasta que, al completar media vuelta, todo el disco aparece iluminado: estamos en Luna llena o plenilunio. A partir de ahí la parte iluminada empieza a reducirse, o a menguar, con una porción oscura de disco lunar que se va extendiendo desde la izquierda hacia la derecha. En el tercer cuarto de vuelta ya solo queda medio disco iluminado (la mitad derecha) y se alcanza el cuarto menguante.

Solo queda un cuarto más de vuelta hasta volver a la fase de Luna nueva y durante ese tiempo la parte brillante del disco lunar se reduce hasta quedar convertida, otra vez, a una lúnula finísima que solo se ve un ratito antes del alba.

La edad de la Luna

No vamos a hablar aquí de los miles de millones de años que tiene nuestro satélite natural, sino del sistema de «edad de la Luna» que sirve para especificar en qué fase se encuentra. La idea es muy sencilla: se trata de dar, en cada momento, cuántos días han pasado desde el último novilunio. Como el ciclo de fases lunares (también llamado mes sinódico) dura, en promedio, 29.53 días, se entiende que la Luna nueva corresponda a cero días de edad (por definición), y que el resto de fases «exactas» (cuartos, plenilunio) coincidan con múltiplos de la cuarta parte de ese periodo, es decir, cada 7 días y 9 horas. Observemos que cada cuarto lunar viene a durar una semana y que un ciclo completo casi coincide con la duración de un mes de calendario. La tabla 2 da la edad de la Luna para algunas fases concretas, con comentarios adicionales.

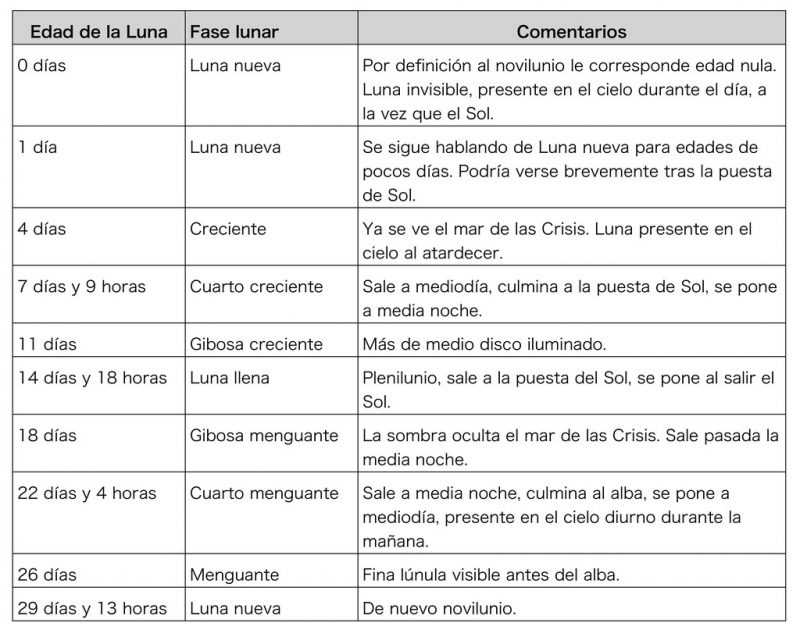
Tabla 2. La edad de la Luna especifica cuánto tiempo ha pasado (medido en días y horas) desde el último novilunio.

Mares lunares

La Luna siempre presenta la misma cara o hemisferio hacia la Tierra, debido a las fuerzas de marea inducidas por nuestro planeta. Esto facilita seguir las fases lunares, porque los cambios de iluminación se van sucediendo por encima de un paisaje de fondo que no cambia, dibujado por los accidentes geográficos de nuestro satélite.

En fase llena se puede contemplar todo el disco de la cara lunar visible y, a simple vista, se distinguen bastantes rasgos que pueden identificarse incluso por su nombre, como se aprecia en las figuras adjuntas.

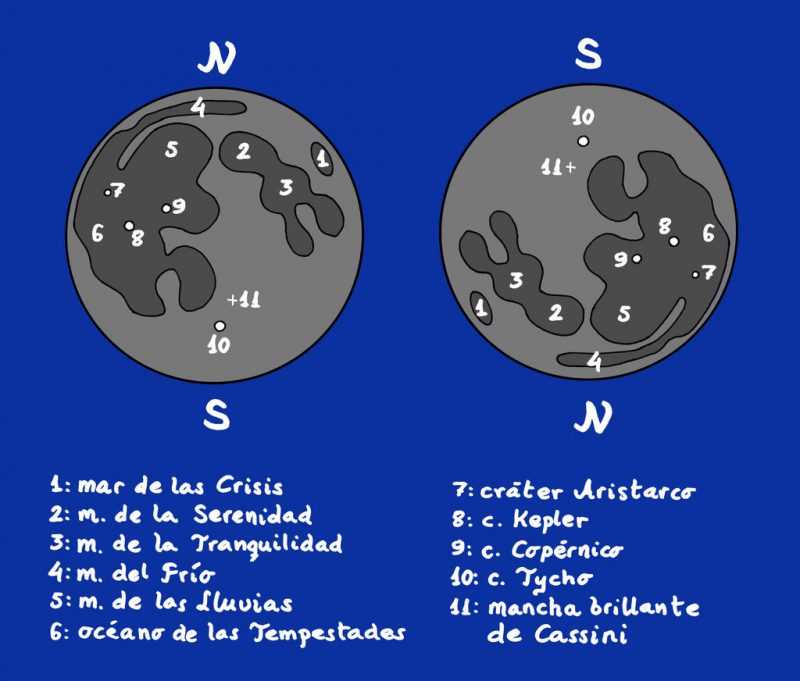
Figura 8. Algunos de los rasgos que pueden observarse a simple vista en el disco de la Luna llena. Izquierda: vista desde el hemisferio norte terrestre. Derecha: vista desde el hemisferio sur terrestre.

Las fases crecientes se inician con la aparición del mar de las Crisis, mientras que el océano de las Tempestades es la última zona sobre la que cae la noche lunar pasado el cuarto creciente, camino de la siguiente Luna nueva.

Quien tenga buena vista, o quien prefiera usar unos simples prismáticos, podrá observar también (preferiblemente en torno a la fase llena) algunos detalles brillantes en el disco lunar, como el cráter Tycho, la «mancha brillante de Cassini» o, en pleno océano de las tempestades, los llamativos puntos claros de los cráteres Copérnico, Kepler y, sobre todo, el blanquísimo Aristarco.