9. Telescopios: óptica

Por David Galadí Enríquez

Todas las personas que se inician en astronomía práctica esperan con ilusión y, a veces, algo de ansiedad, el momento de conseguir su primer telescopio para explorar con los propios ojos los misterios del universo. Es comprensible, pero conviene recomendar un poco de calma y esperar a disponer de algunos conocimientos básicos antes de dar el paso de adquirir un aparato que, según el modelo elegido, puede suponer una inversión considerable. En esta entrega proporcionamos parte de esos conocimientos; en concreto, los que corresponden a la parte óptica de los telescopios, es decir, vamos a describir de una manera elemental qué le hacen estos instrumentos a la luz de los astros. La descripción de los telescopios se completará en el capítulo 10 con el tratamiento de la parte mecánica.

En realidad, los telescopios son tan útiles y tenemos tantas ganas de empezar a usarlos que ya hemos adelantado algunos contenidos. Por ejemplo, los prismáticos son en el fondo pares de telescopios montados en paralelo, de manera que toda la información dada en el capítulo 6 sobre estos aparatos se puede aplicar también a otros telescopios en general. Además, en el capítulo inmediatamente anterior a este dimos algunas indicaciones para usar un telescopio en la observación lunar. Antes o después había que entrar en materia y exponer en detalle la teoría y la práctica de los telescopios amater para uso visual (para «mirar» con ellos), y ese momento ha llegado.

Las estrellas de la óptica

Vamos a estudiar lo que los telescopios le hacen a la luz de los astros. Solo vamos a utilizar un par de fórmulas sencillas y algunos diagramas ópticos simplificados. Pero estos diagramas no se pueden entender bien si no se dedica antes un cierto tiempo a reflexionar sobre qué es una estrella desde el punto de vista de la óptica.

Desde el punto de vista físico, las estrellas son astros autogravitantes compuestos de hidrógeno, helio e impurezas, que emiten luz porque en sus interiores se producen reacciones de fusión nuclear. Pero la naturaleza real, intrínseca, de estos astros tiene muy poca importancia para el asunto que nos ocupa ahora, que se centra más bien en cómo se ven. Desde el punto de vista de la óptica una estrella no es mucho más que una fuente de luz de aspecto puntual situada muy, muy lejos.

Dirá usted que para ese viaje no hacían falta alforjas, porque cualquiera que haya mirado al cielo de noche alguna vez en la vida, aunque sea de la manera más casual, sabe que las estrellas se ven como puntitos. Más o menos brillantes, colocados aquí o allá sobre el negro de la noche, pero puntitos, al fin y al cabo. Sin embargo, sí que hacen falta alforjas para ir un poco más lejos, y justo eso es lo que necesitamos para interpretar bien el funcionamiento de los telescopios.

Si las estrellas son astros enormes, como el Sol, pero muestran un aspecto puntual, eso solo puede deberse a que se encuentran a distancias inmensas. Y en esa gran distancia está la clave de su interpretación correcta desde el punto de vista óptico.

Observemos la figura 1. Arriba a la izquierda se representa una fuente puntual que emite rayos de luz en todas direcciones. Si se considera un lugar de observación muy próximo a la fuente, como el A, los rayos pasan formando un cierto ángulo, divergen entre sí en una cantidad apreciable. El ángulo de divergencia se reduce a medida que crece la distancia entre el objeto emisor y el punto de observación, como se aprecia en la misma figura para los lugares marcados como B y C.

Pero en el caso de las estrellas la distancia se hace enorme, descomunal, cósmica, astronómica, total y absolutamente sobrecogedora. Hemos intentado plasmar esto en el diagrama de la parte inferior de la figura 1 (punto D). La conclusión es que las estrellas son objetos puntuales de los que nos llegan rayos de luz completamente paralelos entre sí.

Figura 1. Diagrama de divergencia de los rayos procedentes de una fuente puntual. El ángulo de divergencia se reduce para distancias crecientes (A, B, C), hasta llegar a hacerse nulo cuando las distancias son colosales (D), como sucede en astronomía.

Hagamos unos números. Si se toma una estrella situada a una distancia intermedia, digamos unos 700 años-luz, entonces dos rayos procedentes de ese astro y que pasen por la Tierra separados entre sí por un metro forman un ángulo igual a tres centésimas de billonésima de segundo de arco (para puristas, 0.03×10^-12 segundos de arco). Recordemos (capítulo 7) que en un grado hay nada menos que 3600 segundos de arco. Se trata de un ángulo ridículo. Es tan pequeño que para que un átomo subtendiera ese diámetro angular habría que colocarlo a casi 700 000 quilómetros, casi el doble de la distancia de la Tierra a la Luna. Es decir: cuando afirmamos que los rayos procedentes de una estrella son paralelos entre sí no se trata de una aproximación, sino de una realidad cabal a todos los efectos prácticos, teóricos y filosóficos. La posible divergencia entre rayos es de una magnitud muy, muy inferior al tamaño de los átomos con que construimos los telescopios.

Es muy importante tomarse en serio esta visión de las estrellas desde el punto de vista óptico. Una estrella cualquiera, esa que vemos como un punto engarzado en la negrura de la esfera celeste, para la óptica no es más que una lluvia de rayos de luz estrictamente paralelos entre sí y que llena todo el paisaje. Al mirar hacia Betelgueuse la pupila atrapa un tubo cilíndrico de rayos de luz, una fracción minúscula de la lluvia de fotones que caen a lo largo de trayectorias paralelas. Pero sobre cada trozo de suelo a nuestro alrededor están incidiendo todo el rato fotones hermanos de los que capturamos, siguiendo siempre caminos paralelos. Y sobre los árboles del horizonte, las cumbres nevadas de los montes o cada palmo cuadrado del mar se repite esa misma lluvia, siempre con esa perfección que mantiene todos los rayos paralelos a los del resto del haz que viene de una sola estrella.

Ya, pero si una estrella consiste en una lluvia de rayos de luz paralelos, ¿cómo es que la percibimos, la vemos, como un puntito de luz? La respuesta está en lo que sucede dentro del ojo. Como se representa en la figura 2, un ojo emétrope y bien enfocado «al infinito», toma ese cilindro de rayos paralelos y lo hace converger para formar un punto sobre la retina. He ahí, reconstruida, nuestra fuente puntual, nuestra estrella.

¿Qué diferencia hay, pues, desde el punto de vista óptico, entre unas estrellas y otras? Sobre todo, dos. Una corresponde a la dirección de la que proviene el haz. Cada estrella provoca una lluvia de fotones que incide sobre la superficie terrestre desde una dirección distinta. Podemos imaginar la esfera celeste como una fuente enorme de lluvias fotónicas, una por cada estrella, cada una diferente a las demás en que sus rayos caen paralelos a líneas distintas.

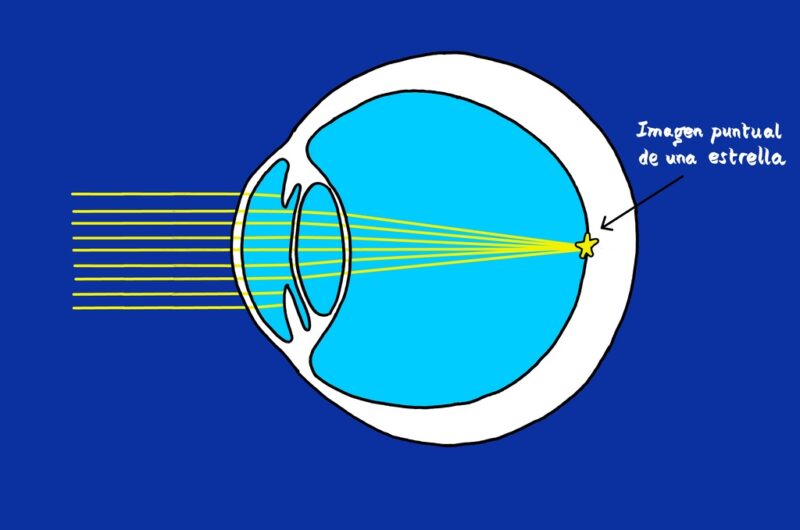
Figura 2. El ojo convierte un haz de rayos de luz paralelos en un puntito sobre la retina. En la figura la luz estelar incide procedente de la izquierda.

La segunda diferencia tiene que ver con la intensidad. Hay estrellas con brillos aparentes mayores y menores, y esto se traduce en lluvias de fotones de distinta intensidad o densidad. Para un astro que aparece muy brillante hay más «rayos por metro cuadrado» que si se considera la lluvia de luz que procede de otra estrella más débil.

Si reunimos las dos diferencias, de dirección y de brillo aparente, en la figura 3 podemos ver lo que sucede dentro del ojo: las lentes frontales capturan cilindros de luz que forman imágenes puntuales en la retina, pero de diferente intensidad dependiendo de la densidad de rayos de una u otra lluvia de fotones y en diferentes posiciones dependiendo del ángulo de incidencia de cada haz.

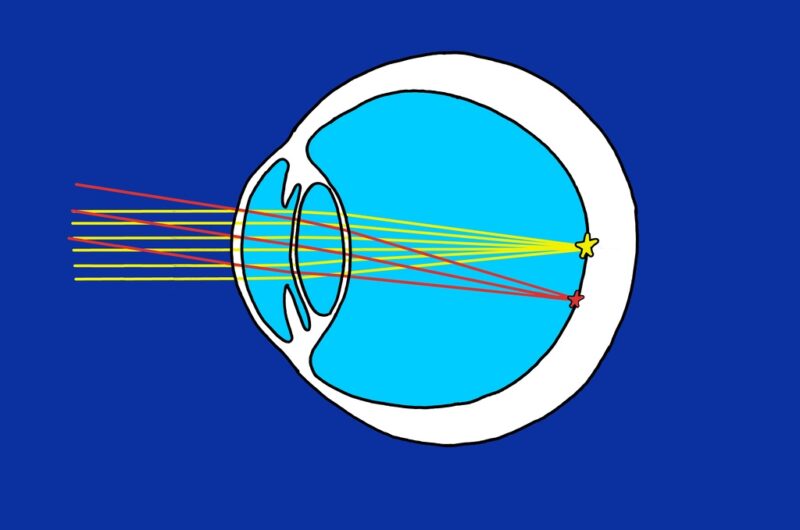
Figura 3. Un ojo observa dos estrellas que difieren entre sí en intensidad (densidad de rayos en cada haz paralelo) y en dirección de procedencia. Observe que las imágenes en la retina se forman invertidas: la estrella más alta forma una imagen en la parte baja del tejido. La luz procede de la izquierda. La estrella con rayos trazados en rojo es más débil que la representada con rayos amarillos.

La figura 3 ilustra otro efecto curioso de la visión humana (y, en realidad, de todos los ojos con estructura análoga a la del nuestro): las imágenes que se forman en la retina están invertidas, «cabeza abajo». Sin embargo, el sistema de proceso de datos cerebral tiene en cuenta esta circunstancia que no conlleva ninguna implicación especial para el tema que nos ocupa.

Ya nos hemos familiarizado con la materia prima sobre la que trabajan los telescopios: las estrellas del cielo consideradas como lluvias de rayos de luz paralelos entre sí. Ahora estamos en mejores condiciones de entender qué hacen nuestros instrumentos ópticos favoritos con esa luz.

Telescopios para observación visual: objetivo y ocular

Volvemos a recordar que en esta guía de inicio nos dedicamos tan solo a los telescopios para uso visual, es decir, considerados como instrumentos en los que colocar el ojo para «mirar» a través de ellos. Cualquier otro uso queda fuera del alcance de este texto como, por ejemplo, la astrofotografía, la toma de secuencias de vídeo o las medidas de intensidad mediante fotómetros o cualquier otro aparato que no sea un ojo humano.

Todos los telescopios astronómicos para uso visual se componen, desde el punto de vista óptico, de dos piezas: el objetivo y el ocular. Esto se aplica también a los prismáticos, que tratamos en el capítulo 6 de esta serie.

Consideremos la imagen arquetípica de un telescopio, la que tiene en mente todo el mundo, incluso las personas con menos interés por la astronomía. Nos imaginamos de inmediato un tubo más o menos largo que lleva una lente en la parte delantera, más ancha, y que tiene otra lente en la parte de detrás, más estrecha, por la que se observa.

En este telescopio canónico, hecho de lentes, el objetivo es la mayor de ellas, la frontal, y recibe este nombre porque se encara, apunta o dirige hacia el objeto observado. El ocular es la lente menor, que cierra el tubo por el extremo opuesto, y debe su nombre justo al hecho de que el ojo se coloca junto a ella a la hora de observar.

Aunque luego veremos que no todos los telescopios están hechos de lentes, podemos partir de este diseño clásico para razonar qué hace un telescopio con la luz de las estrellas.

De entrada, el objetivo actúa como un colector de luz, una especie de embudo que abarca un cilindro de rayos con un tamaño (anchura) igual a su diámetro. La lente objetivo siempre es de carácter convergente y las leyes de la óptica establecen que el tubo de rayos paralelos se convierte en un cono de luz que se concentra en un punto de un plano, el plano focal del objetivo. Si en ese lugar se colocara una pantalla, la estrella se materializaría ahí como un puntito luminoso, exactamente lo mismo que sucede en la retina como consecuencia de las lentes frontales del globo ocular. Si en lugar de una sola estrella (una sola lluvia de rayos paralelos) consideramos dos, con direcciones diferentes y, también, distintas intensidades (distintas densidades de rayos de luz), el resultado son dos imágenes sobre esa pantalla. Esta situación se representa en la figura 4. Observe que, como ocurre en el ojo humano, la posición de las estrellas en el plano focal del objetivo está invertida: la luz que procede de «más arriba» forma la imagen estelar puntual en el plano focal más abajo. La longitud que media entre la lente objetivo y su plano focal se llama distancia focal del objetivo.

Figura 4. Dos haces de luz, cada uno formado por rayos paralelos entre sí, inciden sobre la lente objetivo desde la izquierda. El cilindro de rayos amarillos es paralelo al eje de simetría de la lente y forma una imagen puntual en el centro del plano focal. El otro haz es menos intenso (menos densidad de rayos) e incide bajo un cierto ángulo, desde más arriba, lo que provoca que la imagen estelar correspondiente se forme más abajo en el plano focal. La distancia entre la lente y el plano focal se llama distancia focal.

Pero el telescopio destinado a la observación visual no se utiliza para proyectar con el objetivo imágenes minúsculas en una pantalla ubicada en el plano focal. Bueno, para la toma de fotografías sí suele emplearse así, y en ese caso lo que se sitúa en el plano focal es la superficie del detector. Pero para uso visual lo que se hace es colocar a continuación el segundo elemento óptico, el ocular. Los oculares de los telescopios modernos son siempre lentes convergentes.

Si el ocular es una lente convergente debe ejercer un efecto parecido al del objetivo si se coloca frente a una estrella, frente a una corriente de rayos de luz paralelos entre sí. Colectará una sección de esa lluvia fotónica y la concentrará en su propio plano focal. Las imágenes formadas estarían a una distancia del ocular que recibe el nombre de distancia focal del ocular. Pero los oculares no se usan de este modo. Lo que se hace con ellos es justo lo contrario, es decir: se sitúan a una distancia del plano focal del objetivo que sea igual a la distancia focal del ocular y, de esa manera, los rayos que divergen a partir del plano focal entran al ocular y vuelven a salir del mismo perfectamente paralelos. El ocular convierte la luz convergente de las estrellas ofrecida por el objetivo en una nueva lluvia de fotones lista para que la capte el ojo, como si se tratara del haz luminoso procedente de una estrella natural, un haz que no hubiera pasado por ningún instrumento óptico.

Muchas personas se quedan perplejas cuando se enteran de este detalle sobre el modo de funcionamiento de los telescopios. Si por el objetivo entran rayos de luz estelar paralelos y todo lo que hace el aparato es expulsar por el ocular otro haz de rayos paralelos, ¿qué se gana con ello?

Figura 5. Un telescopio refractor completo: lente objetivo a la izquierda y lente ocular a la derecha. La luz de dos estrellas (dos haces de rayos paralelos) incide desde la izquierda. El tubo de rayos amarillos corresponde a una estrella más brillante porque tiene más densidad de rayos que el rojo, e incide paralelo al eje del telescopio. El cilindro de rayos rojos representa una estrella más débil e incide sobre el objetivo formando siete grados con el eje óptico y con el otro haz: sobre el cielo veríamos las estrellas separadas por siete grados. El ocular recoge la luz estelar concentrada en el plano focal y produce dos tubos de luz. Cada tubo de luz de salida es más denso que el de entrada: las estrellas se abrillantan. El ángulo entre los tubos de luz de salida es mucho mayor que el ángulo que formaban al entrar: se amplía la separación aparente entre las estrellas. Como el objetivo, en este ejemplo, tiene el triple de distancia focal que el ocular, el telescopio es de tres aumentos y el ángulo de salida es el triple que el de entrada. Por el ocular vemos las estrellas separadas un ángulo aparente igual a 3 × 7 = 21 grados. El telescopio da una imagen invertida (la luz estelar roja, que venía de arriba a la entrada, viene desde abajo a la salida).

Brillo aparente y aumento

Pero quien lea esta guía de iniciación dispone ya de conocimientos suficientes para entender una primera ventaja del uso del telescopio. Dijimos antes que cada estrella provoca su propia lluvia de rayos de luz paralelos entre sí, pero que los astros brillantes causan corrientes de fotones con más densidad de líneas. Aquí tenemos la primera, e importantísima, diferencia entre el caudal de luz que entra al telescopio y el que sale. El chorro de luz de salida es más denso que el que entró, es como si todos los rayos que cayeron sobre el objetivo se hubieran concentrado, realmente el efecto se parece al de un embudo, un embudo de luz. Por lo tanto, al colocar el ojo en la salida del telescopio, cerca del ocular, la estrella en cuestión se observará más brillante. ¡El telescopio incrementa el brillo aparente de los astros! Al menos, de los astros puntuales como las estrellas.

Pero la cosa no queda ahí. También hemos comentado que dos estrellas distintas provocan lluvias de fotones que proceden de direcciones diferentes, por eso vemos las estrellas situadas en puntos distintos del cielo, tal y como se aprecia en la figura 3. La figura 5 muestra que los chorros de luz estelar que salen del telescopio no solo son más densos que cuando entraron, sino que, además, forman entre sí ángulos mayores. Si los chorros que entran al globo ocular forman ángulos mayores, las estrellas forman imágenes más separadas en la retina: ¡se aumenta el tamaño aparente de las imágenes! Dos cosas que en el cielo a simple vista aparezcan separadas un cierto ángulo se verán separadas un ángulo mayor al mirar a través del telescopio.

Concluimos que el telescopio cumple, al menos, dos funciones: incrementar el brillo aparente de las estrellas y agrandar el tamaño aparente de las cosas.

Segundos de arco

En el capítulo 1 de esta serie proponíamos medir ángulos en el cielo en grados, usando para ello una regla graduada. Luego, al tratar la contaminación lumínica en el capítulo 7 dividimos cada grado (°) en sesenta trocitos, llamados minutos de arco (‘), y cada minuto de arco se puede subdividir, a su vez, en otros sesenta fragmentos llamados segundos de arco (“). Por muy chiquitito que parezca un segundo de arco, el uso de telescopios nos coloca a menudo en este rango de medidas. Pensemos que el disco del Sol, o el de la Luna, vienen a medir medio grado, o sea, unos 30 minutos de arco, que vienen a ser 1800 segundos de arco. El disco del planeta Júpiter, visto desde la Tierra, tiene un tamaño aparente que ronda el minuto de arco. Muchos cráteres lunares se ven aún menores y conviene ya medirlos en segundos, como ocurre con la separación de muchas estrellas dobles.

Un par de fórmulas

Ha llegado el momento de introducir las dos únicas fórmulas, ambas muy simples, que permiten valorar el funcionamiento de un telescopio en su doble papel de intensificador de estrellas y de ampliador de las imágenes.

Brillo aparente de las estrellas vistas al telescopio

El poder abrillantador de un telescopio se puede valorar especificando la magnitud visual de las estrellas más débiles que puede llegar a mostrar. En el capítulo 3 definimos el sistema de magnitudes estelares usado en astronomía para clasificar el brillo de los astros. Vimos entonces que una vista humana normal, en una noche oscura de gran calidad, puede llegar a percibir, sin ayuda óptica, estrellas hasta de la magnitud 6. Pero hemos aprendido que los telescopios intensifican el brillo aparente de las estrellas, lo que implica que, con ellos, podremos ver astros de magnitudes superiores a 6 y, por supuesto, las que ya captábamos a simple vista se mostrarán aún más brillantes. El problema es más complejo de lo que parece y cualquier respuesta simple tiene que ser, por fuerza, aproximada, pero tanto la teoría como la experiencia indican que la fórmula siguiente arroja resultados razonables. La magnitud límite m, es decir, la de las estrellas más débiles que pueden verse a través de un telescopio con objetivo de abertura (es decir, diámetro) D, medido en milímetros, viene dada por:
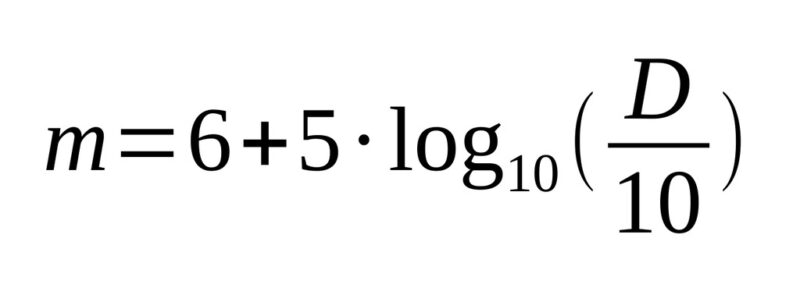Esta expresión presupone que la pupila humana totalmente dilatada mide unos 7 mm, lo cual es algo optimista, y que la magnitud límite sin telescopio asciende a 6, lo cual solo será cierto bajo cielos bastante oscuros. La fórmula incorpora también unas ciertas pérdidas de luz en el interior del telescopio, una circunstancia inevitable y que, por sorprendente que pueda parecer, muchas veces se olvida al tratar este asunto.

Como se ve, la fórmula incorpora un logaritmo decimal. Quienes no estén familiarizados con los logaritmos pueden ignorar la fórmula y consultar, en cambio, la tabla 1 y la gráfica de la figura 6.

Tabla 1. Relación aproximada entre la abertura (diámetro) del objetivo en milímetros y la magnitud límite para observación visual bajo un cielo oscuro. Se acepta una pupila humana de 7 mm, una magnitud límite igual a 6 a simple vista y se incorporan ciertas pérdidas de luz en el interior del telescopio.

Figura 6. Relación aproximada entre la abertura del objetivo en milímetros y la magnitud de las estrellas más débiles que pueden observarse con él, mediante ocular y un ojo con vista normal, en las mismas condiciones indicadas en el pie de la tabla 1.

Por supuesto, el rendimiento puede ser mejor si se trabaja bajo un cielo de calidad excepcional y con una vista anormalmente buena, lo que podría permitir que se parta de una magnitud límite sin ayuda óptica mayor que 6. Si, además, el telescopio es de gran calidad y está bien cuidado y alineado, entonces las pérdidas de luz serán menores. Condiciones contrarias irán en el sentido opuesto, como es natural.

Obsérvese que la magnitud límite depende solamente de la abertura del objetivo, es decir, no cuenta para nada el ocular. Bien, este es un modelo simple, así que algo más tarde matizaremos este aspecto indicando de qué modo tanto la atmósfera como el ocular elegido, es decir, los aumentos, pueden afectar a estos resultados.

Tamaño aparente de los objetos vistos al telescopio

Lo que sí es evidente es que el ocular interviene en el poder de ampliación, en los aumentos del telescopio. La fórmula para calcular el aumento consiste en dividir la distancia focal del objetivo entre la distancia focal del ocular: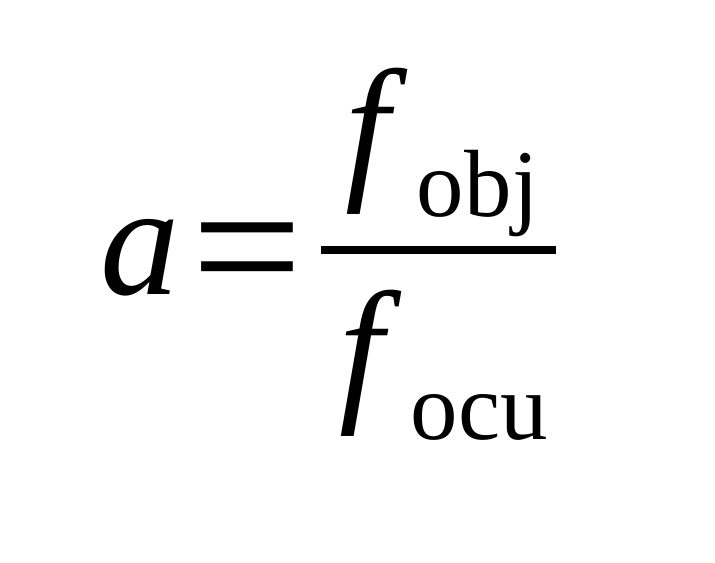Por supuesto, para que la fórmula funcione las dos distancias focales se deben expresar en las mismas unidades, por ejemplo en milímetros.

Todo telescopio debería ir equipado con varios oculares, normalmente tres, o incluso más, aunque se suelen vender con solo uno o dos. El motivo de tener varios no es otro que obtener distintos niveles de aumento colocando oculares con distancias focales más o menos grandes. Saber cuántos aumentos se están usando tiene su importancia y, por eso, todos los telescopios llevan marcado en el tubo, en lugar bien visible, la distancia focal del objetivo, normalmente expresada en milímetros. Del mismo modo, el parámetro más importante de cualquier ocular es su distancia focal, que también está marcada con claridad en el barril del dispositivo.

Figura 7. El telescopio debe mostrar en algún lugar a la vista la distancia focal del objetivo (F) y, también, la abertura (D). En este caso D= 254 mm y F = 1200 mm. El ocular también exhibe de manera muy clara su distancia focal, 25 mm en la imagen. Por tanto, la configuración presentada en la fotografía ofrece 1200 / 25 = 48 aumentos.

Se entiende ahora que los prismáticos sin zum, que tienen tanto objetivos como oculares fijos, no intercambiables, solo puedan ofrecer un número determinado de aumentos, el que figura anotado en la carcasa, como comentamos en el capítulo 6.

Observemos que un telescopio, desde el punto de vista óptico, se puede identificar con el conjunto formado por el objetivo y su juego de oculares intercambiables. Al nivel más elemental, el objetivo queda caracterizado por la abertura (o diámetro) y la distancia focal, mientras que el dato más importante del ocular es su distancia focal. De los dos superpoderes del telescopio, la capacidad para intensificar el brillo aparente de las estrellas depende, en una primera aproximación, tan solo de la abertura y no de la distancia focal, mientras que la capacidad de aumentar el tamaño aparente de los objetos depende de la distancia focal del objetivo (combinada con la del ocular), pero no de la abertura.

¿Cuántos aumentos pongo?: límite de resolución

Esta es una de las preguntas más frecuentes que surgen al iniciarse en la observación visual con telescopio. Las personas no iniciadas tienden a pensar que «cuantos más aumentos, mejor», pero vamos a ver que esto no es así.

Es fácil entender que el número máximo de aumentos tiene que tener un límite. La óptica no es perfecta, es decir, las imágenes que da el telescopio están afectadas por defectos que también se amplían al incrementar los aumentos. Por eso, si nos empeñamos en aplicar un número absurdamente elevado de aumentos, por ejempo 15 000, el resultado solo puede ser una imagen borrosa, confusa y que, además, temblará en el campo de visión con la vibración más mínima del telescopio. Por tanto, podemos plantearnos qué aumento sería el máximo razonable para no empezar a ampliar defectos de las imágenes, con la intención de quedarnos en el intervalo de potencias que pongan de manifiesto los detalles más finos que nuestro telescopio sea capaz de mostrar.

Aquí entra en juego el concepto de resolución. Incluso un telescopio perfecto verá limitada su capacidad de mostrar detalles por motivos físicos (difracción) que no se pueden evitar. El poder de resolución de un objetivo mejora al crecer la abertura. Es decir, telescopios mayores tienden a mostrar detalles más finos. Entre las fórmulas simples que circulan por la bibliografía no da mal resultado la que afirma que la resolución, expresada en segundos de arco, equivale aproximadamente a 140/D, donde D vuelve a ser la abertura medida en milímetros. La tabla 2 y la figura 8 ofrecen algunos números orientativos basados en esta fórmula.

Tabla 2. Resolución teórica, solo por efectos ópticos, en telescopios según su abertura. Los datos son aproximados porque los detalles dependen del diseño óptico del telescopio. Se indican los límites de borrosidad (seeing) normal (2”), buena (1”) y excepcionalmente buena (0.5”). Telescopios de más abertura no mejorarán la resolución más allá de los límites impuestos por la atmósfera.

De modo que la resolución viene limitada por la abertura del telescopio. Podría parecer que para distinguir detalles muy finos en las imágenes bastaría con adquirir un objetivo lo bastante grande. Por ejemplo, la fórmula anterior puede llevar a pensar que basta un telescopio de medio metro de abertura (muy grande, pero no desconocido en el mundo amater) para lograr resoluciones mejores que 0.3 segundos de arco. Y así sucede de verdad para los telescopios situados en el espacio. Pero observamos a través de la atmósfera y las perturbaciones causadas por el aire inducen una borrosidad (en inglés usan el término seeing) inevitable. Por encima de cierta abertura la resolución ya no viene limitada por la óptica, sino por la atmósfera.

Figura 8. La información de la tabla 2 en forma de gráfica: resolución teórica de los telescopios en función de la abertura del objetivo. Las líneas grises horizontales marcan los límites de borrosidad (seeing) normal (2”), buena (1”) y excepcionalmente buena (0.5”). Telescopios de más abertura no mejorarán la resolución más allá de los límites impuestos por la atmósfera.

La borrosidad es más o menos intensa dependiendo de las condiciones de la atmósfera. Una estrella, como buena fuente puntual que es, debería mostrar un aspecto minúsculo si no hubiera aire. Pero cuando su luz cruza la atmósfera la turbulencia hace engordar las estrellas y las convierte en «bolitas» cuyo tamaño aparente se suele medir en segundos de arco. En lugares de observación normales y corrientes, como el interior de una población, no es extraño que las condiciones de turbulencia emborronen cualquier detalle por debajo de dos segundos de arco. En un lugar de observación francamente bueno la borrosidad puede mejorar y reducirse hasta un segundo de arco. Solo en lugares muy buenos y en condiciones realmente muy excepcionales podemos soñar con una borrosidad de tan solo medio segundo de arco, infrecuente incluso en observatorios internacionales de primer nivel.

La clave de los aumentos, en lo que a resolución se refiere, radica en que no tiene sentido ampliar las imágenes mucho más allá de su calidad intrínseca. Entonces, si las estrellas presentan un cierto grado de borrosidad intrínseco, sea debido a la óptica o a la atmósfera, no sirve de nada aplicar unos aumentos tan altos que pongan de manifiesto esa borrosidad, es decir, no tiene sentido ampliar tanto como para que las estrellas dejen de parecer puntuales y empiecen a verse como bolas temblorosas de luz.

Los seres humanos con mejor vista llegan a distinguir en el entorno detalles con el tamaño aparente de un minuto de arco, 1’. Lo normal es no tener una vista tan buena y, además, tampoco hay que exagerar llevándolo todo al extremo: aunque la resolución de un ojo normalito ronde 2’, puede ayudar a captar mejor los detalles ampliar un poco más. De modo que puede tener sentido hacer crecer las estrellas hasta que muestren tamaños aparentes de, digamos 3’, equivalentes a 180”. Por supuesto, aquí hay implícita una cierta decisión arbitraria. Con estos parámetros podríamos definir el aumento resolvente como aquel que, aplicado a un telescopio, amplía las imágenes estelares hasta hacer que su tamaño angular real (debido a la óptica o a la atmósfera) se traduzca en 3’ al mirar por el telescopio. Una simple división nos dice que en condiciones normales, cuando las estrellas miden 2”, el aumento resolvente, o máximo aceptable, está alrededor de 180 / 2 = 90. Sorprendente pero cierto: en condiciones de borrosidad normales, muy frecuentes en el entorno de ciudades y al nivel del mar, raramente se gana en calidad aplicando aumentos por encima de ese valor. En estas condiciones no es raro que al aplicar 100, o incluso 150 aumentos, las imágenes se vean más ampliadas, pero con una calidad degradada y sin que la potencia adicional revele más detalles.

No está de más recordar que para que el telescopio aproveche bien las condiciones de turbulencia, si estas son de unos 2”, se requiere un telescopio de al menos 7 cm de abertura (tabla 2). Cualquier telescopio cuya abertura esté por debajo de ese umbral brindará estrellas más «gordas» aún y, por tanto, su aumento resolvente quedará incluso por debajo de estos límites.

Por supuesto, si las condiciones son realmente buenas y la borrosidad ronda un segundo de arco, entonces podemos alcanzar 180 / 1 = 180 aumentos sin ampliar en exceso los efectos de la turbulencia. Se requiere para ello, además, que el telescopio no degrade la resolución por encima de ese segundo de arco, lo que apunta a telescopios con aberturas en el entorno de 15 cm, o mayores. En lugares muy buenos y bajo condiciones realmente excepcionales, cuando la atmósfera induce una borrosidad de medio segundo de arco, entonces, si el telescopio tiene más de 28 cm de abertura, podemos aplicar hasta 180 / 0.5 = 360 aumentos.

Llegamos a la conclusión de que los límites de resolución intrínsecos impuestos por la óptica de los telescopios o por la atmósfera implican unos umbrales, a su vez, sobre los aumentos máximos que es razonable aplicar a un telescopio, y que los números que resultan son bastante moderados, entre unos 100 y 300 aumentos, según las condiciones, o incluso menos para telescopios de abertura muy escasa.

Pero no se vayan todavía, aún hay más. Hasta ahora hemos valorado los límites a los aumentos en lo que se refiere a la resolución, pero queda tratar qué implica la ampliación de las imágenes en cuanto al brillo aparente de las imágenes.

¿Cuántos aumentos pongo?: brillo aparente de las estrellas

Hemos visto que los telescopios incrementan el brillo aparente de las fuentes puntuales, de las estrellas, porque actúan como un «embudo óptico» que condensa toda la luz que llueve sobre el objetivo en un cilindro de luz de salida que contiene más densidad de rayos.

Mientras la pupila del ojo reciba todo el chorro de luz que sale del telescopio, y mientras siga siendo válida la hipótesis de que la estrella es una fuente puntual, entonces estaremos aprovechando todo el poder intensificador de brillo del telescopio para las estrellas.

En la entrega dedicada a la observación con prismáticos introdujimos ya el concepto de pupila de salida, que no es más que el grosor, el diámetro, del cilindro de luz que emerge por el ocular del telescopio. El diámetro de la pupila de salida se calcula de manera muy sencilla dividiendo la abertura del objetivo entre el número de aumentos.

En principio, mientras toda la luz entre en el ojo, las fuentes puntuales no pierden brillo aparente, así que poner muchos aumentos no debería debilitar las estrellas. Pero atención, porque las estrellas dejan de ser fuentes puntuales si se amplían tanto que el ojo las empiece a ver como bolitas, o sea, cuando se alcanza o supera el aumento resolvente tratado en el apartado anterior. Vemos, pues, que el aumento resolvente no solo marca el límite razonable de aumentos para ampliar detalles en las imágenes, sino que también marca la frontera más allá de la cual las estrellas empiezan a perder brillo, porque ya no son fuentes puntuales (vemos su «tamaño») y, al ampliarlas más, su caudal de luz empieza a desparramarse sobre un área aparente más amplia y pierde densidad.

Si el aumento resolvente establece el límite superior de aumentos para no perder luz de fuentes puntuales, el diámetro de la pupila del ojo marca un límite inferior. En efecto, no tiene sentido configurar la combinación de objetivo y ocular de manera que el chorro de luz de salida sea más grueso que la pupila del ojo porque, en ese caso, parte de la luz no entra en el globo ocular y se pierde.

Al tratar los prismáticos indicamos que los ojos juveniles pueden alcanzar diámetros pupilares de hasta 7 mm, mientras que ese valor decrece con la edad y puede limitarse a 5 mm para personas mayores. Unos 6 mm de diámetro suponen una buena solución de compromiso y basaremos los cálculos que siguen en esa referencia.

La tabla 3 da algunos números que se plasman gráficamente en la figura 9. Si en el apartado anterior nos hemos llevado la sorpresa de que no conviene abusar de los aumentos por motivos de resolución, ahora vemos que tampoco interesa aplicar demasiado pocos, para no perder capacidad de recolección de luz.

Por supuesto, en ocasiones se pueden superar estos límites por arriba o por abajo por motivos diversos. Por ejemplo, en ocasiones puede interesar aplicar aumentos inferiores al equipupilar para lograr un campo de visión mayor aunque sea a costa de perder brillo aparente. En observación de estrellas dobles se puede ir más allá del aumento resolvente para facilitar medidas de separación entre componentes, aunque sea a costa de convertir las estrellas en borrones con aspecto horroroso.

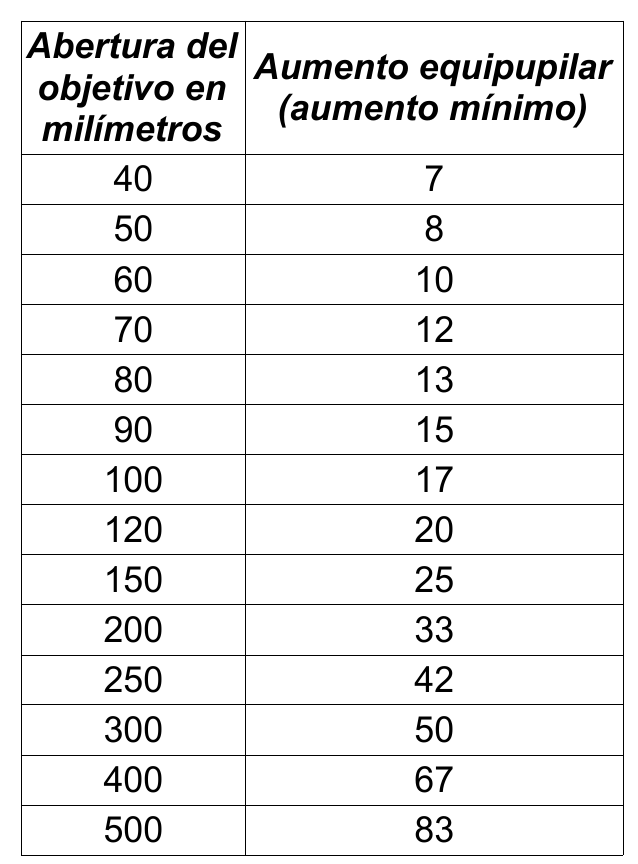
Tabla 3. El aumento equipupilar para cada abertura. Estos aumentos hacen que la pupila de salida del telescopio sea de 6 mm. Si se aplican menos aumentos se perderá luz, por eso se pueden interpretar como los aumentos mínimos recomendables para cada objetivo.

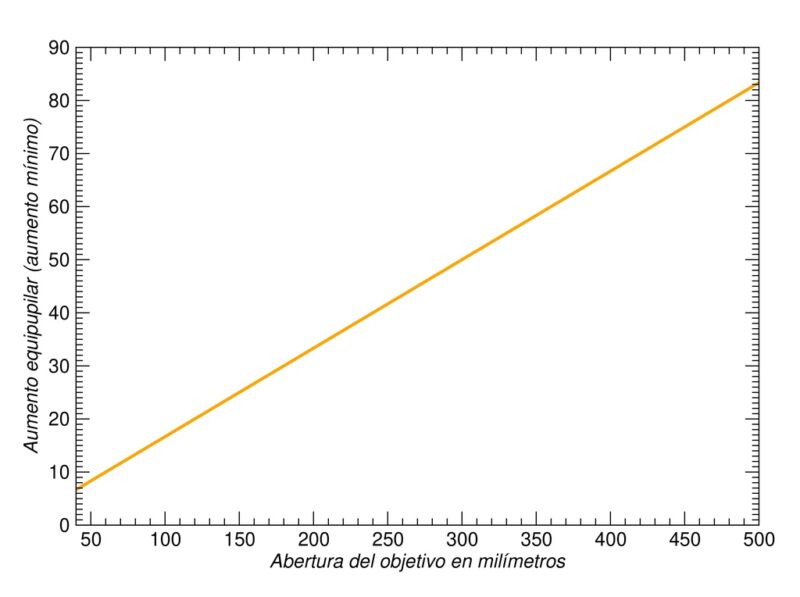
Figura 9. El aumento equipupilar como función de la abertura (para una pupila de ojo de 6 mm). Se puede interpretar como el aumento mínimo recomendable: por debajo de estos valores los objetos, tanto extensos como puntuales, pierden brillo aparente.

¿Cuántos aumentos pongo?: brillo aparente de los objetos difusos

En los apartados anteriores nos hemos referido a las estrellas como objetos puntuales. Pero en el cielo no solo hay objetos puntuales, también están la Luna, los planetas y otros objetos como nebulosas o galaxias, que tienen un aspecto extenso, para nada puntual.

Todas las consideraciones relativas a resolución espacial se aplican también a estos objetos. Por tanto, un exceso de aumentos más allá del aumento resolvente no mejorará, sino que empeorará, la apariencia de la Luna, los planetas y las nebulosas. Pero ¿qué decir en cuanto a su brillo aparente?

A este respecto el comportamiento de las imágenes es totalmente distinto al de los objetos puntuales. Las estrellas pueden resistir la ampliación hasta que dejen de verse como puntitos, momento en el cual empiezan a perder brillo si aumentamos todavía más. Pero esto mismo les sucede a los objetos extensos desde el primer momento. Más aumentos siempre debilitan el brillo de las nebulosas, las galaxias, la Luna o los planetas. En el caso de la Luna esto puede ser una bendición, porque con aumentos bajos llega a deslumbrar, y para los planetas puede convenir más resolución, más aumento, aunque sea a costa de rebajar algo el brillo superficial. Pero en nebulosas y galaxias la pérdida de luz suele ser letal. Por tanto, para la observación de este tipo de objetos interesa siempre aplicar los mínimos aumentos posibles, sin descender por debajo del aumento mínimo, el aumento equipupilar. Esto es verdad siempre que el objeto que se pretende observar muestre un tamaño razonable: objetos muy pequeñitos, como la nebulosa Anular de la Lira, pueden requerir cierto aumento aun a costa de perder brillo. Como los telescopios grandes tienen aumentos equipupilares mayores, deducimos que las grandes aberturas tienen entre sus ventajas la de permitir más aumentos sin perder luz en el caso de objetos difusos.

Sin embargo, los telescopios comerciales suelen tener distancias focales largas que dificultan obtener aumentos bajos, porque para ello se requerirían oculares de distancias focales también muy largas, los cuales no se fabrican. De hecho, no hay en el mercado demasiados oculares con focales superiores a 40 mm y ninguno que rebase en mucho los 50 mm. Esto hace que la mayoría de telescopios de focal larga tengan que utilizarse, para observación visual, con aumentos superiores al equipupilar, lo que puede admitirse para fuentes puntuales, pero reduce el rendimiento para observar objetos difusos.

Resumen sobre aumentos

Podemos sintetizar todo lo tratado en los apartados anteriores en una serie de puntos:

• Normalmente no hay motivos para utilizar un aumento inferior al equipupilar. Cada objetivo tiene un aumento mínimo marcado por este umbral. Con menos aumentos todo pierde brillo aparente.
• Al poner aumentos superiores al equipupilar, los objetos extensos (Luna, planetas, nebulosas, galaxias) siempre pierden brillo aparente, pero no necesariamente las estrellas.
• No tiene sentido superar el aumento resolvente. Más allá del aumento resolvente las vistas se vuelven temblorosas, débiles y borrosas, y las estrellas pierden brillo.
• El umbral de aumentos altos depende de la abertura del objetivo para objetivos pequeños, pero el factor limitante suele ser la turbulencia de la atmósfera, sobre todo para objetivos grandes.

Por ejemplo, con un telescopio de 15 cm de abertura siempre trabajaremos, aproximadamente, entre 25 aumentos (umbral equipupilar) y 180 aumentos (aumento resolvente para esa abertura, que coincide además con la borrosidad atmosférica en noches buenas, un segundo de arco).

Telescopios hechos con espejos

Hasta ahora hemos razonado sobre telescopios compuestos por lentes, conocidos como refractores. Pero el poder de convergencia de rayos que proporciona una lente también se puede obtener por medio de espejos cóncavos. La mayoría de telescopios amater emplean al menos un espejo y hay buenas razones para ello.

El motivo principal está en la aberración cromática. Es bien sabido que cuando la luz atraviesa un vidrio no solo se desvía (refracción) sino que, además, se descompone en colores (dispersión), como vemos cuando la luz cruza un prisma de cristal, una botella llena de agua o cuando llueve y las gotas de agua descomponen la luz en el arco iris.

Ese mismo fenómeno sucede en los objetivos formados por lentes, lo que da lugar a imágenes con aureolas de colores y de mala calidad óptica. Este fenómeno se conoce como aberración cromática. La aberración cromática se puede atenuar utilizando lentes objetivo compuestas de más de un elemento, cada uno de ellos de características distintas y calculadas de manera que la aberración cromática de una pieza compense, al menos en parte, la de la otra. Los objetivos refractores de dos elementos (dos lentes juntas) se llaman acromáticos, pero están afectados de una cierta aberración cromática residual. Resultan prácticamente perfectos, para observación visual, los objetivos refractores de tres elementos llamados apocromáticos, pero también es cierto que son muy caros. Entre ambas categorías están los objetivos de tipo ED, a veces denominados semiapocromáticos, de dos elementos pero que utilizan vidrios especiales de muy bajo poder de dispersión.

Pero otro modo de eludir la aberración cromática consiste en utilizar espejos cóncavos. Los objetivos basados en espejos se llaman reflectores, y dominan el panorama totalmente por encima de ciertas aberturas. De hecho, todos los grandes telescopios de investigación son reflectores.

Los reflectores puros más sencillos y populares para observación visual son los de tipo Newton, compuestos por un espejo primario cóncavo y un espejo secundario plano que desvía la luz hacia un lateral. En los telescopios de este diseño se mira por un costado y el ocular está colocado en esa posición lateral y cerca de la boca de entrada del tubo, por donde entra la luz al sistema.

Figura 10. Esquema de un telescopio reflector de tipo Newton.

Los reflectores son más baratos que los refractores para grandes aberturas. Aun así, para aberturas intermedias interesa, a veces, elaborar objetivos que son una combinación de lentes y espejos, los llamados objetivos catadióptricos. Un espejo de bajo coste, esférico, se encarga de las funciones principales, mientras que una lente frontal, llamada placa correctora, rectifica algunas de las aberraciones del espejo esférico sin introducir demasiada aberración cromática. Estas combinaciones dejan de ser prácticas por encima de 40 cm de abertura, tamaño a partir del cual encontramos en el mercado casi solo telescopios reflectores a los que se pueden añadir más o menos elementos refractores complementarios, pero ya como parte del tren óptico de salida, cerca del ocular.

El mercado ofrece dos tipos principales de objetivos catadióptricos: los de Maksútov y los de diseño Schmidt-Cassegrain. En ambos casos la luz atraviesa primero la placa correctora, luego incide sobre el espejo primario y, finalmente, da con un espejo convexo colocado sobre la misma placa correctora que devuelve la luz hacia atrás. Estos diseños resultan muy compactos y en ellos se mira por la parte de atrás, como en los refractores.

El diseño Maksútov usa una placa correctora cóncava vista desde fuera, y que lleva «pintado» un círculo de aluminio que hace de espejo secundario. Como este espejo secundario es totalmente solidario a la placa correctora, es imposible que se produzcan desalineamientos. Como la placa correctora es muy masiva, cuando la abertura crece más allá de, digamos unos 18-20 cm las aberraciones cromáticas y el peso se tornan excesivos, por lo que no hay telescopios de este diseño que superen esas dimensiones.

Figura 11. Esquema de telescopios catadiópticos de tipo Maksútov (arriba) y Schmidt-Cassegrain (abajo). Aunque los espejos secundarios se representan separados de la placa correctora en ambos casos, lo más frecuente en el diseño de Maksútov es que el espejo secundario consista en una zona aluminizada de la propia lente, lo que hace imposible su desalineamiento.

La variante Schmidt-Cassegrain tiene el espejo secundario adosado a la placa pero sin formar parte solidaria de ella, lo que puede dar lugar a desalineamientos. La placa es menos masiva y esto permite alcanzar aberturas mayores en productos comerciales, superiores incluso a 40 y 50 cm, sin que se introduzcan aberraciones cromáticas considerables.

Aplicación al mundo real

Con todo lo aprendido podríamos acudir a un catálogo de productos de cualquier comercio y valorar algunos parámetros. Por ejemplo, sucede con frecuencia que los oculares que se ofrecen con los telescopios no son del todo satisfactorios y conviene adquirir al menos uno adicional para cubrir el intervalo de aumentos mínimos. Una elección sensata sería disponer de un ocular que proporcione el aumento equipupilar o aumento mínimo, otro que brinde el aumento resolvente (o máximo) para condiciones de turbulencia buenas (un segundo de arco de borrosidad) y otro intermedio.

Si se toma como referencia el ocular de distancia focal más grande que puede conseguirse con facilidad, de unos 40 mm, y una pupila de salida óptima de 6 mm, entonces, para obtener el aumento equipupilar, deberíamos optar por telescopios que tengan un cociente entre distancia focal y abertura (la llamada relación focal) inferior a 6.5, pero el mercado suele ofrecer valores bastante superiores: basta dividir distancia focal del objetivo entre abertura del objetivo para un abanico de diseños comerciales para apreciar que muy a menudo se supera este umbral, lo que significa que no es posible obtener el aumento equipupilar, el idóneo para observar objetos difusos débiles.

En la tabla 4 hemos representado algunos modelos comerciales realmente existentes y para cada uno de ellos damos abertura y distancia focal del objetivo, tipo de diseño óptico, relación focal, aumentos mínimo y máximo (en las condiciones indicadas, 6 mm de pupila de salida y 1” de borrosidad traducida en 3’ en las imágenes), las distancias focales de los oculares correspondientes, y algunos comentarios. Damos el enlace a la hoja de cálculo original, en formato ods de LibreOffice, que permitirá modificar parámetros y hacer cálculos para otros modelos de telescopio: puede cambiar la pupila del ojo, el nivel de borrosidad (seeing) inducido por la atmósfera, la resolución a la que aspira en la imagen ofrecida por el telescopio (tamaño aparente de las imágenes estelares) y, luego, puede modificar abertura y distancia focal de los telescopios, o añadir otros nuevos a través de estos dos datos (el resto de columnas, salvo la de diseño óptico, las calcula el sistema).

Tabla 4. Valores de algunos de los parámetros comentados en el texto, para modelos de telescopio realmente existentes en el mercado. Las cifras resultan de los parámetros que constan en la cabecera: pupila humana de 6 mm, borrosidad buena (o sea, 1”), aumento resolvente calculado para convertir la borrosidad en una imagen de 3’. Puede modificar los parámetros si descarga la hoja de cálculo original, en formato ods para LibreOffice.

En la próxima entrega de la serie estudiaremos la parte mecánica de los telescopios, la montura y sus tipos. Con ello quedarán completadas las nociones elementales sobre telescopios en iniciación a la astronomía.

Bibliografía y recursos

Enlace a la hoja de cálculo para valorar distintos parámetros a partir de las características de los objetivos. El documento tiene el formato ods del sistema de ofimática de código libre y libre distribución LibreOffice.
https://elseptimocielo.fundaciondescubre.es/files/2022/09/telescopios.zip

D. Galadí-Enríquez y J. Gutiérrez Cabello, De la Tierra al universo: Astronomía general teórica y práctica, 2ª. edición, Ediciones Akal. Los capítulos sobre telescopios de este libro, en particular el 6, abarcan parte de los contenidos de esta entrega.

M. A. Covington, Telescopios modernos para aficionados, Ediciones Akal. El título hacía plena justicia al contenido de la obra en el momento de su publicación en el año 2005. A pesar de la edad, todavía la mayor parte del libro mantiene toda la actualidad porque se basa en principios generales: la primera parte, 130 páginas del total de 200 de la obra, es imperecedera y extremadamente recomendable para profundizar en muchos de los conceptos tratados en este artículo.