
Así sabemos que la Tierra es redonda
La humanidad sabe que la Tierra tiene forma redonda, más o menos esférica, desde hace milenios. A veces se esgrimen las fotos de la Tierra tomadas desde el espacio como demostración de la esfericidad de la Tierra, y no está mal, pero ese tipo de pruebas no estaba al alcance de quienes nos precedieron hace siglos y, aun así, no les cabía ninguna duda de que habitamos un mundo redondo. Y no les cabía duda porque hay muchas pruebas, indicios y datos que prueban la redondez de la Tierra sin necesidad de tecnología costosa ni de conocimientos científicos o matemáticos complejos. Esas pruebas tienen que seguir accesibles en la actualidad, o incluso más a mano, gracias a la tecnología moderna. Vamos a repasar algunas de ellas. Incluso la vida cotidiana nos enseña la forma verdadera de nuestro planeta.
Salidas y puestas del Sol y de la Luna
Un fenómeno tan cotidiano y hermoso como las salidas y las puestas de Sol se convierten en un enigma indescifrable a no ser que la Tierra sea redonda. Es cierto que amaneceres y atardeceres pueden explicarse con una Tierra estática y un cielo en movimiento, pero de ningún modo con una Tierra plana.
El simple hecho cotidiano de que el Sol salga desde debajo del horizonte y se oculte tras él en cada jornada nos dice muchas cosas. ¿Dónde va cuando se esconde, de dónde sale? ¿Por qué aparece y desaparece en instantes distintos en cada lugar del planeta? Este último detalle no era nada sencillo de comprobar en el pasado porque requiere telecomunicaciones instantáneas que de las que solo disponemos desde la invención del telégrafo o el teléfono, pero ahora cualquiera puede constatar que los amaneceres y atardeceres ocurren en Mallorca 47 minutos antes que en Lisboa, y aquí está la clave, extremadamente fácil de demostrar en la actualidad, de que el mundo tiene que ser redondo. Por supuesto, las salidas y puestas de la Luna conducen a los mismos argumentos.
El recorrido del Sol y la Luna por el firmamento
Las cosas que nos sobrevuelan, como pájaros, aviones, satélites artificiales o los cuerpos celestes, cumplen una ley a la que nos habituamos intuitivamente desde la infancia: todos esos objetos se mueven aparentemente más rápido cuando pasan justo por encima, y se desplazan sobre el paisaje más despacio cuando están lejos. Pensemos, por ejemplo, en un avión cuya trayectoria lo lleve a sobrevolar el lugar de observación. Cuando empieza a verse muy lejos, quizá cerca del horizonte, parece que avanza muy poco a poco, casi está clavado en un punto fijo del cielo.
Pero poco a poco se aproxima y su movimiento empieza a manifestarse. A la vez, puede que la estela blanca que deja (compuesta sobre todo de hielo de agua, y de ninguna cosa rara más o menos) se vaya viendo más grande. También el propio cuerpo del avión cambia de tamaño aparente. Cuando pasa justo por encima de la cabeza, el movimiento aparente es el más veloz de todo el recorrido, la estela se aprecia con toda claridad y hasta puede que veamos las alas del aparato. Desde ahí, el espectáculo se invierte y el desplazamiento aparente se vuelve a hacer más lento a medida que el avión se aleja, se aproxima en apariencia al horizonte y se torna más pequeñito.
Este panorama que tenemos tan interiorizado se aplica a todo lo que vuela, como pájaros, por ejemplo. Cuanto más bajo, cuanto más cercano esté el objeto volador, más intenso se torna el contraste entre la rapidez con que rebasa la vertical de lugar y la lentitud con que parece moverse cuando está lejos. Dicho de otro modo: si aceptamos una velocidad promedio común para todos los aviones (digamos, 900 km/h), el medir con qué ritmo van cruzando el cielo, cuántos grados recorren cada segundo, ofrece una manera de saber a qué distancia están. Los prismáticos suelen llevar indicado el campo de visión que abarcan. Si tenemos unos prismáticos con 5 grados de campo y un avión lo cruza, de lado a lado, en 35 segundos, unos cálculos muy simples (accesibles al alumnado de secundaria) muestran que su distancia ronda los 100 km.
Para cosas más alejadas, más elevadas, como satélites artificiales (que se ven cada noche, por cierto, y cada vez más), el contraste de velocidad aparente entre el objeto lejano y el objeto cercano se atenúa y, de hecho, quienes observan satélites artificiales de noche a simple vista acaban desarrollando una percepción subjetiva que permite distinguir en pocos segundos qué es un satélite artificial y qué un avión, solo por estos detalles.
Es bastante sencillo comprobar que la Luna y el Sol cruzan el firmamento cotidiano sin cambiar de velocidad aparente en ningún momento. Esto puede constatarse con un telescopio sencillo o con relojes de Sol (¡basta mirar las sombras durante un día!): el ritmo de movimiento aparente del Sol no cambia en absoluto, para nada, a lo largo de la jornada, y este se desplaza por el cielo con una velocidad aparente constante de, más o menos, quince grados cada hora. Con la Luna pasa lo mismo. De nuevo, estas observaciones cotidianas no permiten distinguir si es la Tierra la que rota o si, por el contrario, es el firmamento entero el que gira a nuestro alrededor. Pero el comportamiento del movimiento aparente de los dos astros principales del cielo solo se puede entender si ambos se encuentran muy, muy lejanos, a distancias inconcebibles cuya magnitud verdadera no se puede evaluar con medios simples, pero argumentos basados en este ritmo de movimiento aparente uniforme garantizan que tanto la Luna como el Sol deben encontrarse, como mínimo, a cientos de miles de quilómetros de distancia.
La distancia al Sol
Acabamos de ver que el hecho de que el Sol recorra el cielo con un ritmo uniforme implica que tiene que encontrarse muy muy lejos. Ahora damos un paso más y vemos cómo esa observación es incompatible con la posibilidad de que la Tierra sea plana. El experimento de Eratóstenes resulta tan simple y contundente que se ha convertido en un tema clásico de la divulgación científica, como ejemplo de cómo la astucia humana puede llegar a descubrir cosas sorprendentes del mundo con medios, a veces, muy rudimentarios. Eratóstenes midió nada menos que el radio del globo terrestre. Este experimento se ha emulado en la actualidad muchas veces como recurso didáctico para enseñanza secundaria, con campañas para la medida de la sombra de un palo a lo largo del día desde distintos lugares de la Tierra. Luego, al poner en común los resultados, se concluye que el Sol se veía en direcciones distintas sobre el cielo (alturas diferentes sobre el horizonte) desde cada emplazamiento, y de esa diferencia de posiciones aparentes se deduce el radio de la esfera terrestre.
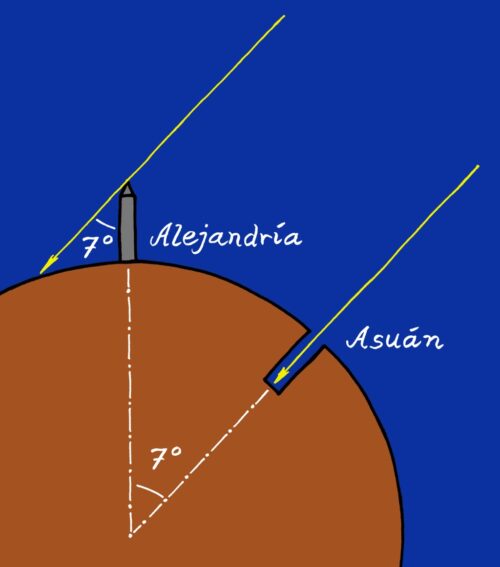
El experimento de Eratóstenes: en el día del solsticio de verano, el Sol del mediodía brilla vertical sobre Asuán, de manera que ilumina el fondo de los pozos, mientras que se observa apartado siete grados del cenit visto desde Alejandría. La explicación natural es que la Tierra es redonda, y que siete grados de latitud cubren la distancia lineal entre las dos localidades.
El experimento sale mejor cuanto más separados estén los lugares de observación, pero si se usa el palo de una escoba o de un recogedor como gnomon y se compara la longitud de la sombra vista desde Algeciras (extremo sur de la península Ibérica) y desde Oviedo (extremo norte), los datos son ya lo bastante significativos y obvios para ofrecer una idea aproximada del tamaño del planeta. La diferencia de latitud entre esas dos poblaciones asciende a algo más de siete grados, que es el resultado de la comparación de las sombras, mientras que distan entre sí, en línea recta, unos 800 km. De ahí se deduce que cada grado de diferencia en latitud equivale a unos 115 km, así que 360 grados dan unos 40 000 km y eso conduce a un radio de algo más de 6000 km para el planeta. ¡Tan simple como mirar la sombra de un recogedor en el patio de la escuela!
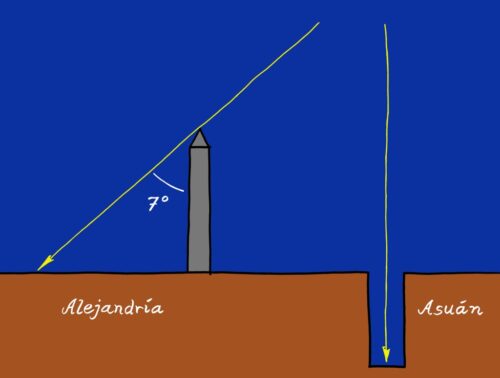
Si se admite que la Tierra es plana, entonces solo cabe interpretar el experimento de Eratóstenes en términos de un Sol muy cercano. Tan cercano, que visto desde Alejandría y Asuán debe cambiar de posición aparente en el cielo nada menos que en siete grados, lo que lo situaría a unos miles de quilómetros de distancia.
Cualquier intento de interpretar estos resultados en términos de una Tierra plana concluye con el resultado de que el cambio aparente de posición del Sol visto desde lugares distintos se debe a que nuestra estrella se encuentra muy cerca. Se trataría de un simple caso de perspectiva, del mismo modo que dos personas separadas entre sí unos cuantos metros ven la torre de la iglesia del pueblo proyectada sobre sitios distintos del horizonte lejano.
Pero sucede que, si al mirar al Sol desde Oviedo y desde Algeciras, ciudades separadas por 800 km en línea recta, el Sol cambia de posición aparente en siete grados (¡catorce veces su diámetro aparente!), la trigonometría elemental (accesible al alumnado de secundaria) conduce a una conclusión inapelable: el Sol tiene que estar a 6300 km sobre la superficie de la Tierra plana. No es sorprendente este resultado: tiene que salir una cantidad igual al radio de la Tierra que se derivaría al interpretar los datos en términos del experimento de Eratóstenes en una Tierra redonda. Pero ya hemos visto en el apartado anterior que la hipótesis de la cercanía del Sol es incompatible con el hecho de que siga un ritmo de movimiento uniforme por el cielo. Por tanto, solo cabe concluir que la Tierra no puede ser plana, sino redonda.
Para la Luna la cosa es más clara aún, porque tiene que estar más cerca que el Sol, dado que sabemos que de vez en cuando pasa por delante del mismo. Pero… ¿cuánto más cerca? Observaciones sencillas, cotidianas, no permiten deducir este dato.
Ni el Sol ni la Luna cambian de tamaño aparente a lo largo de la jornada
Es verdad que no hay maneras sencillas, accesibles al público general, para medir la distancia real hasta el Sol o la Luna. Pero sí hay al menos otro modo más, bastante trivial, de comprobar que ambos objetos tienen que estar muy lejos: medir su tamaño aparente.
Del mismo modo que antes dedujimos la lejanía de la estrella y del satélite porque ni el Sol ni la Luna se mueven por el cielo como lo tendrían que hacer si estuvieran muy cerca, ahora estamos en condiciones de predecir que, si colocamos estos astros a unos cuantos miles de quilómetros, ambos deberían cambiar de tamaño aparente con el paso del día. Igual que el avión se agranda en apariencia cuando nos sobrevuela para luego empequeñecerse a medida que se aleja camino del horizonte, el Sol y la Luna deberían hacer lo mismo, si realmente flotaran a 3000 km por encima de la Tierra.

Estrellas circumpolares. Imagen: Pixabay.
Por cierto, que si el Sol estuviera a poco más de 3000 km de distancia, dado que subtiende un diámetro aparente de medio grado, resulta muy fácil deducir que su tamaño real ascendería a poco más de 50 km. Un Sol de 50 km de diámetro.
Pues ese tamaño aparente de medio grado debería cambiar, disminuir, a medida que el Sol se aleja hacia el horizonte. Si admitimos que el Sol está colgado de un mecanismo que hace que recorra quince grados de longitud geográfica cada hora (se trata de un promedio), eso, en la zona de Europa (por ejemplo) significa desplazarse a unos 1300 km/h.
De nuevo está al alcance del alumnado de secundaria deducir que, si se compara el tamaño aparente máximo del Sol supuesto cercano (a mediodía) con el que debería mostrar tres horas más tarde (si se aleja a 1300 km/h manteniendo la altitud), resulta que en esas tres horas el disco solar debería haberse encogido en más de un 60% de su tamaño aparente. ¡El Sol y la Luna, a la puesta o a la salida, deberían aparecer con la mitad del tamaño aparente que tienen cuando brillan altos!
Comprobamos de nuevo que observar la realidad cotidiana aporta indicios imposibles de ignorar que apuntan a que tanto el Sol como la Luna están muy lejos, hasta el extremo de que no se aprecia cambio de tamaño aparente en ellos entre la culminación (paso por el meridiano) y sus salidas y puestas, lo cual solo es compatible con una distancia enorme para ambos cuerpos, lo que de nuevo conduce a la conclusión de que los observamos desde un mundo redondo.
¿Qué son los polos celestes?
La observación astronómica más elemental muestra que la esfera celeste parece girar en torno a la Tierra. Es cierto que en la antigüedad se admitía que toda esa esfera era real, sólida, y giraba cada día alrededor de una Tierra… esférica. Pero hoy sabemos que no hay esfera celeste, que las estrellas son soles situados a distancias inconcebibles de la Tierra, y que su movimiento diurno aparente se debe, sin más, a la rotación de la esfera terrestre alrededor de su eje. La rotación terrestre tiene como consecuencia más directa que el firmamento parece girar. Este dato tan elemental solo puede explicarse con sencillez si el mundo es redondo.
Reparemos, para empezar, en que las estrellas parecen girar en torno a la Tierra y lo hacen de manera solidaria, como una verdadera esfera, con dos polos o centros de rotación: los polos celestes norte y sur. Esto se comprueba tomando una foto de larga exposición de noche, apuntando desde el hemisferio norte de la Tierra a la estrella Polar, para captar ese giro coordinado y acompasado de todas las estrellas alrededor de ese astro que, por casualidad, está clavado en el cielo en el lugar hacia el que apunta el eje de rotación de la Tierra.
Lo anterior podría llegar a explicarse de un modo más o menos rebuscado a partir de un modelo de Tierra plana. Pero si se da un paso más ya solo cabe admitir que la Tierra tiene que ser redonda. Veamos: ¿por qué al desplazarnos sobre la Tierra hacia el norte o hacia el sur, cambia de posición aparente el polo celeste? Esta observación es tan sencilla que incluso quienes se desplazan entre la península Ibérica y las islas Canarias ya pueden darse cuenta de que la estrella Polar se ve en posiciones distintas desde un lugar y otro. En una Tierra redonda el asunto no requiere mucho más comentario: cambiar de latitud hace que veamos partes distintas del cielo y que el polo celeste cambie también de ubicación, de hecho el polo celeste dista del horizonte un ángulo igual a la latitud del lugar. Sería una misión imposible explicar el cambio de posición aparente del polo norte celeste en una Tierra plana.
Además, al irse desplazando del norte hacia el sur van apareciendo constelaciones nuevas, regiones del cielo totalmente inaccesibles desde Europa, Asia o América del Norte. Desde Chile, Argentina o Australia se ve el polo celeste sur y todas las constelaciones que lo rodean, como el Centauro o la Cruz del Sur. ¿Por qué cambia el panorama celeste, por qué se ven regiones nuevas del cielo mientras que otras desaparecen, si la Tierra es plana? De nuevo, solo la forma redonda del planeta ofrece una respuesta satisfactoria.
Se aleja un barco
Ir a la playa es una forma de viajar mucho más barata y cotidiana que tomar un avión para cubrir las distancias intercontinentales necesarias para detectar el cambio de posición de los polos celestes y la aparición de constelaciones nuevas hacia el sur o hacia el norte. Pero resulta que también la playa nos demuestra que la Tierra es redonda o, al menos, que no puede ser plana. Todas las culturas mundiales con tradición marinera saben lo que vamos a explicar ahora, desde tiempos inmemoriales.

Los barcos que se alejan de la costa desaparecen tras el horizonte como si se hundieran, de modo que lo último que se ve de ellos es su parte más alta. Desde el barco se aprecia un efecto semejante en las masas de tierra. Este efecto indica que el mundo no puede ser plano.
Porque vuelve a ser un tópico en enseñanza y divulgación explicar que los barcos que se alejan del puerto llegan a desaparecer tras el horizonte como si se hundieran, primero deja de verse el casco y solo al final se deja de ver la punta de los mástiles, un efecto geométrico trivial de la curvatura de la Tierra.
Esta observación se torna más sencilla hoy día porque disponemos de prismáticos asequibles, y porque hay grandes estructuras verticales, como chimeneas o molinos de viento, que también presentan estos efectos en las condiciones adecuadas. La conclusión es tan inapelable y sencilla hoy día como lo era en tiempos de los primeros navegantes griegos y fenicios que surcaban el Mediterráneo.
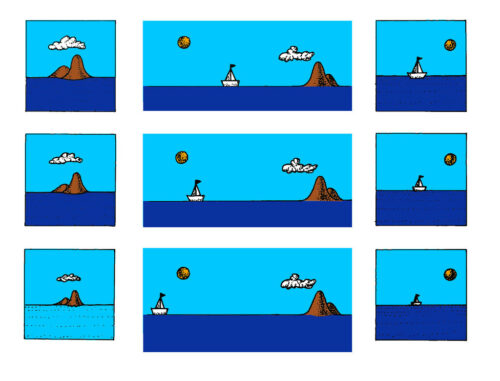
En un mundo plano, los barcos deberían empequeñecerse al alejarse, pero sin esconderse jamás tras el horizonte. Un efecto semejante debería suceder con la costa vista desde los barcos. Nada de esto sucede de este modo, por la sencilla razón de que el mundo no es plano.
Las mareas
La explicación de las mareas oceánicas, la subida y bajada rítmica de los mares al compás del movimiento de la Luna y del Sol, se complicaría muchísimo si no se aceptara que la Tierra es redonda. No existe aún, ni parece que pueda existir, una teoría viable de las mareas en una Tierra plana.
¿Qué son los satélites artificiales y cómo funciona el GPS?
Algunas pruebas de que la Tierra es redonda ya estaban accesibles en la antigüedad y son lo bastante convincentes como para que la verdad se supiera hace siglos. Pero resulta que hoy día tenemos pruebas adicionales, proporcionadas por la tecnología y la ciencia, y que acceder a ellas resulta también muy sencillo, en algunos casos. Veremos algunas de ellas y la primera la brindan los satélites artificiales.
Cada noche es posible ver muchos satélites artificiales. Aparecen como puntitos de luz que se mueven por el cielo, entre las estrellas, en línea recta. Se trata de objetos de metal de varios metros de tamaño que lucen porque todavía les da la luz del Sol. Los satélites artificiales giran alrededor de la Tierra en órbitas regidas por la mecánica celeste Esta observación solo puede hacerse en las primeras horas de la noche, tras el ocaso, o en las últimas, antes del amanecer, porque en las horas centrales de la noche los satélites siguen estando ahí, pero no les da la luz del Sol y, por eso, no se ven brillar. Explicar qué son los satélites artificiales, o qué hacen ahí, resulta imposible si no se admite que la Tierra es redonda.
Y, cómo no, entre los satélites artificiales destacan los de las constelaciones dedicadas al posicionamiento global, como los satélites GPS estadounidenses, los Galileo europeos, el sistema Glonass ruso o los Beidou chinos. Todos los teléfonos móviles modernos incorporan sistemas de posicionamiento global que se basan en la existencia de satélites artificiales, en que la Tierra es redonda y en que existe (y funciona) una teoría de la gravitación universal. Nada de esto funcionaría en un mundo plano.
Vuelo Johannesgurbo-Sidney, listo para embarcar
La aviación comercial es otra tecnología moderna que solo tiene sentido si la Tierra es redonda. Podríamos partir de la idea de que la Tierra es plana y que se parece, grosso modo, al emblema de la Organización de las Naciones Unidas. En esta visión el polo norte ocupa el centro de una Tierra plana con forma de disco, en la que paralelos de latitud sucesivos se van volviendo cada vez más grandes. Podríamos aceptar que, en este marco, el cuadrante de meridiano entre el polo y el ecuador tiene los 10 000 km que se han medido con no poco esfuerzo. Según eso, cálculos geométricos elementales, al alcance del alumnado de secundaria, indican que el ecuador terrestre tendría 63 000 km de perímetro, más de un 50 % adicional a su longitud verdadera.

La bandera de las Naciones Unidas. Imagen: Pixabay.
Por supuesto que la visión plana, «proyectada», del mundo tiene sus problemas. Porque en la realidad esférica de la Tierra los paralelos que hay al sur del ecuador se van reduciendo hasta llegar a un punto en el polo sur, es decir, cada paralelo austral tiene menor perímetro que el anterior. Pero en la Tierra plana que estamos suponiendo ahora sucede justo lo contrario: los paralelos se van agrandando al sur del ecuador hasta alcanzar dimensiones ridículamente enormes, una cosa realmente espectacular.
Si admitimos el sistema de proyección más simple, en el que cada meridiano radial tiene un tamaño de 110 km por cada grado (en números redondos), entonces resulta lo dicho antes, que del polo norte al ecuador hay 90° y, por tanto, 10 000 km, y quedarían otros tantos hasta llegar al borde externo del disco, allá donde estaría la Antártida.
Una concepción del mundo tan extraña conduce a dificultades insalvables en cuanto se hacen los intentos más elementales por aclarar cuáles son las distancias y los rumbos en este modelo, lo cual conduce a la conclusión inevitable de que el planeta Tierra no puede ser así, que tiene que ser redondo. Porque la idea de extender, expandir, ampliar el hemisferio sur de la Tierra en un modelo plano lleva a un incremento enorme de las distancias en el hemisferio austral, algo que contradice toda la experiencia de quienes pilotan y utilizan vuelos comerciales en esa zona de la Tierra.

Tabla 1. Los vuelos intercontinentales en el hemisferio austral solo tienen sentido si la Tierra es redonda.
En el hemisferio norte el problema es muy secundario, porque, como se ve en la tabla 1, la deformación causada por la proyección de la Tierra esférica sobre un plano no afecta demasiado en esta zona. Si pensamos en la ruta aérea Nueva York – Tokio, la distancia real es de 10 800 km, mientras que el modelo de Tierra plana lo alargaría hasta 11 000 km, lo cual puede ser aceptable. La velocidad media real de los vuelos entre estas dos ciudades asciende a 830 km/h, con lo que se cubre el trayecto en 13 horas. El modelo de la Tierra plana requeriría aviones algo más veloces, que tendrían que desplazarse a 850 km/h para cubrir la distancia, incrementada artificialmente por la proyección, en el mismo tiempo.
La cosa cambia de manera radical en el hemisferio sur. La distancia verdadera entre Johannesburgo (Sudáfrica) y Sidney (Australia) asciende a 11 000 km, comparable, por tanto, a la que media entre Nueva York y Tokio. Aun así, los vuelos comerciales que operan actualmente entre ambos aeropuertos cubren el tramonen un tiempo menor que el dedicado a viajar de la Gran Manzana a Japón, porque lo hacen en unas 12 horas. Esto conduce a una velocidad media para el vuelo África-Australia de 930 km/h.
Pues bien, si insistiéramos en admitir que la Tierra es plana, esto expandiría la distancia entre Johannesburgo y Sidney hasta más que duplicarla, con una separación de 23 500 km. Como es un hecho empírico y constatable por quienes toman el avión que el vuelo se completa en 12 horas, llegamos al resultado ineludible de que en el universo de la Tierra plana los aviones comerciales de la línea Johannesburgo-Sidney son supersónicos, puesto que viajan a 2000 km/h (recordemos que la velocidad del sonido ronda los 1200 km/h). Ya no vuelan más las maravillas aeronáuticas supersónicas como el Concorde o el Túpolev 144: el hecho de que la tecnología moderna nos permita viajar Johannesburgo a Sidney en 12 horas con aviones convencionales solo tiene explicación si, de verdad, la Tierra es redonda.
Últimos publicados Ver más

Una auténtica (e inquietante) estrella de Navidad
Barwell, condado de Leicestershire, Inglaterra 24 de diciembre de 1965, 14:20 (UTC): Todo preparado para celebrar la Nochebuena. La particular humedad del ambiente inglés, en…

Navidad en una guardería estelar
Seguro que alguna vez ha jugado a «unir puntos», el tradicional juego de papel y lápiz cuya recompensa es la aparición de una figura oculta….

